下面是小明設計的“三角形一邊上的高”的尺規作圖：
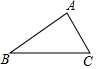
| 已知：△ABC 求作：△ABC的邊BC上的高AD 作法：（1）分別以B和C為圓心，BA，CA為半徑作弧，兩弧相交于點E， （2）作直線AE交BC于點D 所以，線段AD就是所求作的高 |
（1）利用直尺和圓規補全圖形（要求保留作圖痕跡）
（2）小明給出作圖設計的理由如下：
連接BE，CE．
∵BA=BE，
∴點B在線段AE的垂直平分線上（依據1），
同理可證：點C也在線段AE的垂直平分線上．
∴BC垂直平分AE（依據2）．
∴線段AD是△ABC的邊BC上的高．
上面說理過程中的“依據1”，“依據2”分別指什么？
依據1：
到線段兩個端點距離相等的點在線段的垂直平分線上
到線段兩個端點距離相等的點在線段的垂直平分線上
；依據2：
兩點確定一條直線
兩點確定一條直線
．【考點】作圖—基本作圖；線段垂直平分線的性質．
【答案】到線段兩個端點距離相等的點在線段的垂直平分線上；兩點確定一條直線
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：74引用：2難度：0.5
相似題
-
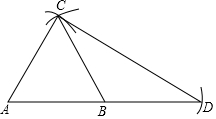1．小明在學了尺規作圖后，通過“三弧法”作了一個△ACD，其作法步驟是：
①作線段AB，分別以A，B為圓心，AB長為半徑畫弧，兩弧的交點為C；
②以B為圓心，AB長為半徑畫弧交AB的延長線于點D；
③連接AC，BC，CD．
下列說法不正確的是（ ）發布：2025/5/25 4:30:1組卷：670引用：6難度：0.5 -
2．如圖，在Rt△ABC中，∠C=90°，以頂點A為圓心、適當長為半徑畫弧，分別交AC、AB于點M、N，再分別以點M、N為圓心，大于MN的長為半徑畫弧，兩弧交于點P，作射線AP交邊BC于點D，若CD=4，AB=5，則△ABD的面積是 ．12發布：2025/5/25 4:30:1組卷：131引用：1難度：0.7 -
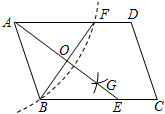3．如圖，在平行四邊形ABCD中，AD∥BC，以點A為圓心，AB長為半徑畫弧交AD于點F，分別以點B，F為圓心，大于的長為半徑作弧，兩弧交于點G，作射線AG交BC于點E，交BF于點O．12BF
（1）求證：△ABE是等腰三角形；
（2）若BF=6，AB=5，求AE的長．發布：2025/5/25 5:0:4組卷：57引用：5難度：0.5