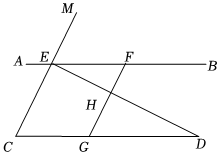
如圖，已知點E，F在直線AB上，點G在線段CD上，ED與FG交于點H，∠C=∠EFG，∠CED=∠GHD．
（1）試判斷∠AED與∠D之間的數量關系，并說明理由；
（2）若∠EHF=80°，∠D=30°，求∠AEM的度數．
【考點】平行線的判定與性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/3 8:0:9組卷：330引用：9難度：0.7
相似題
-
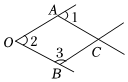1．如圖，一個由4條線段構成的“魚”形圖案，其中∠1=50°，∠2=50°，∠3=130°，找出圖中的平行線，∠ACB的度數，并說明理由．
解：OA∥BC，OB∥AC．
理由：∵∠1=50°，∠2=50°，
∴∠1=∠2（等量代換）
∴OB∥AC． （ ），
∴∠3+∠ACB=180°，（ ），
∴∠ACB=°，
∵∠2=50°，∠3=130°，
∴∠2+∠3=180°，
∴OA∥BC．（ ）．發布：2025/6/7 21:0:1組卷：680引用：6難度：0.9 -
2．下列結論中，正確的是（ ）
發布：2025/6/7 22:30:2組卷：1140引用：6難度：0.8 -
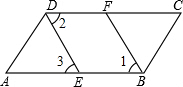3．如圖，∠ABC=∠ADC，BF、DE分別平分∠ABC與∠ADC，DE∥FB．求證：AB∥DC．
請根據條件進行推理，得出結論，并在括號內注明理由．
證明：∵BF、DE分別平分∠ABC與∠ADC，
∴∠1=∠ABC，∠2=12∠ADC．（12）
∵∠ABC=∠ADC，
∴．
∵DE∥FB
∴∠1=∠3，（）
∴∠2=．（等量代換）
∴AB∥CD．（）發布：2025/6/7 21:30:1組卷：637引用：4難度：0.3