【圖形定義】
有一條高線相等的兩個三角形稱為等高三角形．
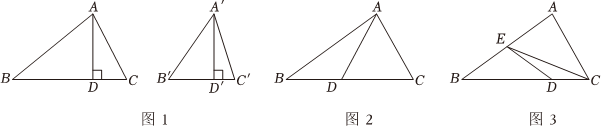
例如：如圖1，在△ABC和△A′B′C′中，AD，A′D′分別是BC和B′C′邊上的高線，且AD=A′D′，則△ABC和△A′B′C′是等高三角形．
【性質探究】
如圖1，用S△ABC，S△A′B′C′分別表示△ABC和△A′B′C′的面積．
則S△ABC=12BC?AD，S△A′B′C′=12B′C′?A′D′．
∵AD=A′D′，
∴S△ABC：S△A′B′C′=BC：B′C′．
【性質應用】
（1）如圖2，D是△ABC的邊BC上的一點．若BD=3，DC=4，則S△ABD：S△ADC=3：43：4．
（2）如圖3，在△ABC中，D，E分別是BC和AB邊上的點．若BE：AB=1：2，CD：BC=1：3，S△ABC=1，則S△BEC=1212，S△CDE=1616．
【提示】∵△BEC和△ABC是等高三角形，∴S△BEC：S△ABC=BE：AB=1：2．∴S△BEC=12S△ABC=12×1=12．∵△CDE和△BEC是等高三角形，∴S△CDE：S△BEC=CD：BC=1：3．∴S△CDE=13S△BEC=13×12=16．
（3）如圖3，在△ABC中，D，E分別是BC和AB邊上的點，若BE：AB=1：m,CD：BC=1：n,S△ABC=a,則S△CDE=amnamn．
【提示】∵△BEC和△ABC是等高三角形，∴S△BEC：S△ABC=BE：AB=1：m.∴S△BEC=1mS△ABC=1m×a=am．∵△CDE和△BEC是等高三角形，∴S△CDE：S△BEC=CD：BC=1：n.∴S△CDE=1nS△BEC=1n×am=amn．
S
△
ABC
=
1
2
BC
?
AD
S
△
A
′
B
′
C
′
=
1
2
B
′
C
′
?
A
′
D
′
1
2
1
2
1
6
1
6
S
△
BEC
=
1
2
S
△
ABC
=
1
2
×
1
=
1
2
S
△
CDE
=
1
3
S
△
BEC
=
1
3
×
1
2
=
1
6
a
mn
a
mn
S
△
BEC
=
1
m
S
△
ABC
=
1
m
×
a
=
a
m
S
△
CDE
=
1
n
S
△
BEC
=
1
n
×
a
m
=
a
mn
【考點】三角形綜合題．
【答案】3：4；；；
1
2
1
6
a
mn
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/15 5:0:1組卷：50引用：1難度：0.5
相似題
-
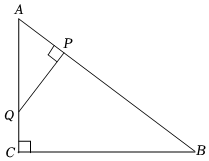1．如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，動點P從點A出發沿線段AB以每秒3個單位長的速度運動至點B，過點P作PQ⊥AB交射線AC于點Q，設點P的運動時間為t秒（t＞0）．
（1）線段AQ的長為 ，線段PQ的長為 .（用含t的代數式表示）
（2）當△APQ與△ABC的周長的比為1：4時，求t的值．
（3）設△APQ與△ABC重疊部分圖形的面積為S，求S與t之間的函數關系式．發布：2025/6/25 4:0:1組卷：19引用：1難度：0.3 -
2．如圖，在△ABC中，BC=5，AD⊥BC，BE⊥AC，AD，BE相交于點O，BD：CD=2：3，且AE=BE．
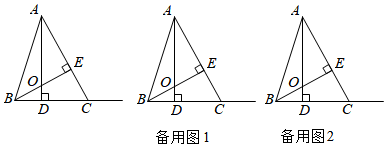
（1）求線段AO的長；
（2）動點P從點O出發，沿線段OA以每秒1個單位長度的速度向終點A運動，動點Q從點B出發沿射線BC以每秒4個單位長度的速度運動．P，Q兩點同時出發，當點P到達A點時，P，Q兩點同時停止運動．設點P的運動時間為t秒，△AOQ的面積為S，請用含t的式子表示S，并直接寫出相應的t的取值范圍；
（3）在（2）的條件下，點F是直線AC上的一點，且CF=BO，是否存在t值，使以點B，O，P為頂點的三角形與以點F，C，Q為頂點的三角形全等？若存在，請直接寫出符合條件的t值；若不存在，請說明理由．發布：2025/6/25 5:0:1組卷：191引用：3難度：0.4 -
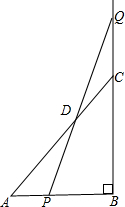3．已知等腰直角△ABC的直角邊AB=BC=10cm,點P，Q分別從A．C兩點同時出發，均以1cm/s的相同速度做直線運動，已知P沿射線AB運動，Q沿邊BC的延長線運動，PQ與直線AC相交于點D．設P點運動時間為t,△PCQ的面積為S．
（1）求出S關于t的函數關系式．
（2）當點P在線段AB上時，點P運動幾秒時，S△PCQ=S△ABC？14
（3）作PE⊥AC于點E，當點P．Q運動時，線段DE的長度是否改變？證明你的結論．發布：2025/6/23 23:0:10組卷：243引用：1難度：0.1