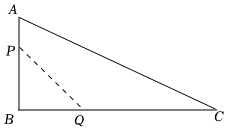
如圖，在△ABC中，∠B=90°，AB=12cm,BC=24cm,動點P從點A開始沿邊AB向點B以2cm/s的速度移動，動點Q從點B開始沿邊BC向點C以2cm/s的速度移動，如果P，Q兩點分別從A，B兩點同時出發，設運動時間為x s.
（1）用含x的式子表示：AP=2x2xcm,BP=（12-2x）（12-2x）cm,BQ=4x4xcm,S△PBQ=（-4x2+24x）（-4x2+24x）cm2，S四邊形APQC=（4x2-24x+144）（4x2-24x+144）cm2；
（2）當△PBQ的面積為32cm2時，求運動時間；
（3）四邊形APQC的面積能否等于172cm2？若能，求出運動的時間；若不能，說明理由．
【考點】四邊形綜合題．
【答案】2x；（12-2x）；4x；（-4x2+24x）；（4x2-24x+144）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：68引用：1難度：0.6
相似題
-
1．如圖，已知矩形ABCD中，AB=4，AD=m,動點P從點D出發，在邊DA上以每秒1個單位的速度向點A運動，連接CP，作點D關于直線PC的對稱點E，設點P的運動時間為t（s）．
（1）若m=6，求當P，E，B三點在同一直線上時對應的t的值．
（2）已知m滿足：在動點P從點D到點A的整個運動過程中，有且只有一個時刻t,使點E到直線BC的距離等于3，求所有這樣的m的取值范圍．發布：2025/6/13 13:0:4組卷：3236引用：5難度：0.1 -
2．閱讀材料題：
浙教版九上作業本①第18頁有這樣一個題目：已知，如圖一，P是正方形ABDC內一點，連接PA、PB、PC，若PC=2，PA=4，∠APC=135°，求PB的長．
小明看到題目后，思考了許久，仍沒有思路，就去問數學老師，老師給出的提示是：將△PAC繞點A順時針旋轉90°得到△P'AB，再利用勾股定理即可求解本題．請根據數學老師的提示幫小明求出圖一中線段PB的長為．
【方法遷移】：已知：如圖二，△ABC為正三角形，P為△ABC內部一點，若PC=1，PA=2，PB=，求∠APB的大小．3
【能力拓展】：已知：如圖三，等腰三角形ABC中∠ACB=120°，D、E是底邊AB上兩點且∠DCE=60°，若AD=2，BE=3，求DE的長．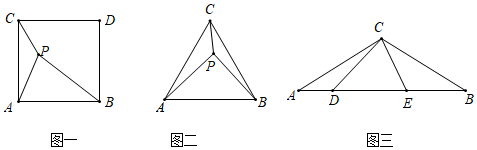
發布：2025/6/13 9:0:1組卷：508引用：3難度：0.1 -
3．已知四邊形ABCD是正方形，點F為射線AD上一點，連接CF并以CF為對角線作正方形CEFG，連接BE，DG．
（1）如圖1，當點F在線段AD上時，求證：BE=DG；
（2）如圖1，當點F在線段AD上時，求證：CD-DF=BE；2
（3）如圖2，當點F在線段AD的延長線上時，請直接寫出線段CD，DF與BE間滿足的關系式．發布：2025/6/13 7:0:2組卷：429引用：3難度：0.2