如圖1，在Rt△ABC中，∠A=90°，AB=AC，點D，E分別在邊AB，AC上，AD=AE，連接DC，點M，P，N分別為DE，DC，BC的中點．
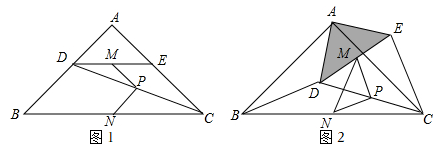
（1）觀察猜想：圖1中，請判斷線段PM與PN的數量關系和位置關系，并說明理由．
（2）探究證明：把△ADE繞點A逆時針方向旋轉到圖2的位置，連接MN，BD，CE，判斷△PMN的形狀，并說明理由．
【答案】（1）PM=PN，PM⊥PN，理由見解析過程；
（2）△PMN是等腰直角三角形，理由見解析過程．
（2）△PMN是等腰直角三角形，理由見解析過程．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：132引用：3難度：0.6
相似題
-
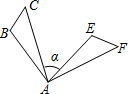1．如圖，△ABC繞點A順時針旋轉80°得到△AEF，若∠B=100°，∠F=50°，則∠α的度數是．發布：2025/7/1 13:0:6組卷：1099引用：19難度：0.7 -
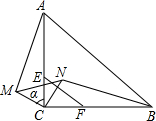2．如圖，已知，在△ABC中，CA=CB，∠ACB=90°，E，F分別是CA，CB邊的三等分點，將△ECF繞點C逆時針旋轉α角（0°＜α＜90°），得到△MCN，連接AM，BN．
（1）求證：AM=BN；
（2）當MA∥CN時，試求旋轉角α的余弦值．發布：2025/6/25 6:30:1組卷：2475引用：59難度：0.5 -
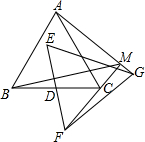3．如圖，△ABC，△EFG均是邊長為2的等邊三角形，點D是邊BC、EF的中點，直線AG、FC相交于點M．當△EFG繞點D旋轉時，線段BM長的最小值是（ ）發布：2025/6/25 6:0:1組卷：5912引用：58難度：0.5