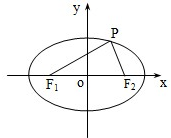
已知點P在橢圓x249+y224=1上，F1、F2是橢圓的焦點，且PF1⊥PF2，求
（1）|PF1|?|PF2|
（2）△PF1F2的面積．
x
2
49
+
y
2
24
=
1
【考點】三角形的面積公式．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：164引用：3難度：0.5
相似題
-
1．在△ABC中，a,b,c分別是角A，B，C的對邊，若b=1，c=
，3，則S△ABC=（ ）A=π3發布：2024/12/3 8:0:32組卷：4引用：1難度：0.9 -
2．凸四邊形PABQ中，其中A、B為定點，AB=
，P、Q為動點，滿足AP=PQ=QB=1．3
（1）寫出cosA與cosQ的關系式；
（2）設△APB和△PQB的面積分別為S和T，求S2+T2的最大值，以及此時凸四邊形PABQ的面積．發布：2024/11/11 8:0:1組卷：123引用：4難度：0.5 -
3．中國南宋大數學家秦九韶提出了“三斜求積術”，即已知三角形三邊長求三角形面積的公式：設三角形的三條邊長分別為a、b、c,則三角形的面積S可由公式
求得，其中p為三角形周長的一半，這個公式也被稱為海倫?秦九韶公式，現有一個三角形的邊長a、b、c滿足a=3，b+c=5，則此三角形面積的最大值為（ ）S=p（p-a）（p-b）（p-c）發布：2024/10/18 7:0:2組卷：7引用：1難度：0.7