提出問題：
在4×4的正方形方格紙上，各個小正方形的頂點稱為格點，以格點為頂點的等腰直角三角形共有幾個？
問題探究：
為了解決上面的問題，我們先從最簡單的情形入手，從中找到解決問題的方法．
探究一：
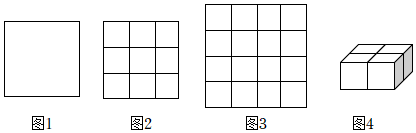
如圖1在1×1的正方形方格紙上，以格點為頂點的線段長度可取2個數值：1，

1

2

+

1

2

=

2

，以這些線段組成的等腰直角三角形按三邊長來考慮可以分為以下一種情況：1、1、

2

．
當斜邊長為

2

時，斜邊一定是1×1正方形的對角線，這樣的線段有2條，每條這樣的線段對應著兩個等腰直角三角形，共有2×2=4個．
故在1×1的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為4個．
探究二：
在2×2的正方形方格紙上，以格點為頂點的線段長度可取5個數值：1，2，

1

2

+

1

2

=

2

，

1

2

+

2

2

=

5

，

2

2

+

2

2

=

2

2

．以這些線段組成的等腰直角三角形按三邊長來考慮可以分為以下三種情況：1、1、

2

；

2

、

2

、2；2、2、

2

2

．
（1）當斜邊長為

2

時，斜邊一定是1×1正方形的對角線，這樣的線段有8條，每條這樣的線段對應著兩個等腰直角三角形，共有8×2=16個．
（2）當斜邊長為2時，圖形中長為2的線段有6條，其中有4條在2×2正方形的四周上，每條這樣的線段對應著一個等腰直角三角形；另有2條在2×2正方形的內部，每條這樣的線段對應著兩個等腰直角三角形，共有4×1+2×2=8個．
（3）當斜邊長為

2

2

時，斜邊一定是2×2正方形的對角線，這樣的線段有2條，每條這樣的線段對應著兩個等腰直角三角形，共有2×2=4個．
故在2×2的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為16+8+4=28個．
探究三：
如圖2在3×3的正方形方格紙上，以格點為頂點的線段長度可取

9

9

個數值．以這些線段組成的等腰直角三角形按三邊長來考慮可以分為以下五種情況：1、1、

2

；

2

、

2

、2；2、2、

2

2

；

5

、

5

、

10

；3、3、

3

2

．
（1）當斜邊長為

2

時，斜邊一定是1×1正方形的對角線，這樣的線段有18條，每條這樣的線段對應著兩個等腰直角三角形，共有18×2=36個．
（2）當斜邊長為2時，圖形中長為2的線段有16條，其中有

8

8

條在3×3正方形的四周上，每條這樣的線段對應著一個等腰直角三角形；另有

8

8

條在3×3正方形的內部，每條這樣的線段對應著兩個等腰直角三角形，共有

8+8×2=24

8+8×2=24

個．
（3）當斜邊長為

2

2

時，斜邊一定是2×2正方形的對角線，這樣的線段有8條，每條這樣的線段對應著兩個等腰直角三角形，共有8×2=16個．
（4）當斜邊長為

10

時，圖形中長為

10

的線段有12條，其中有8條對應著一個等腰直角三角形；
有4條對應著兩個等腰直角三角形，共有8×1+4×2=16個．
（5）當斜邊長為

3

2

時，斜邊一定是3×3正方形的對角線，這樣的線段有2條，每條這樣的線段對應著兩個等腰直角三角形，共有2×2=4個．
故在3×3的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為

36+24+16+16+4=96

36+24+16+16+4=96

個．
問題解決：
如圖3在4×4的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為

244

244

個．
拓展延伸：
如圖4在2×2×1的長方體中，以格點為頂點（每個1×1×1小正方體的頂點均為格點），并且以等腰直角三角形為底面的直三棱柱的個數為

48

48

個．