2022-2023學年山東省青島大學附中九年級（上）期初數學試卷

一.選擇題（共8小題）（每小題0分）

• 1．2022年北京冬奧會在北京，張家口等地召開，在此之前進行了冬奧會會標征集活動，以下是部分參選作品，其文字上方的圖案是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：532引用：10難度：0.9

  解析

• 2．下列運算正確的是（　　）

  A．（-3xy）2=3x2y2	B．3x2+4x2=7x4
  C．t（3t2-t+1）=3t3-t2+1	D．（-a3）4÷（-a4）3=-1
  組卷：846引用：11難度：0.8

  解析

• 3．下列命題：①

  4

  的算術平方根是2；②菱形既是中心對稱圖形又是軸對稱圖形；③天氣預報說明天的降水概率是95%，則明天一定會下雨；④若一個多邊形的各內角都等于108°，則它是正五邊形，其中真命題的個數是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：682引用：5難度：0.6

  解析

• 4．射擊時，子彈射出槍口時的速度可用公式v=

  2

  as

  進行計算，其中a為子彈的加速度，s為槍筒的長．如果a=5×10⁵m/s²，s=0.64m,那么子彈射出槍口時的速度（用科學記數法表示）為（　　）

  A．0.4×103m/s

  B．0.8×103m/s

  C．4×102m/s

  D．8×102m/s
  組卷：1117引用：10難度：0.7

  解析

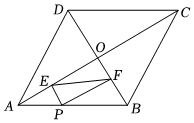• 5．如圖，菱形ABCD的對角線AC，BD相交于點O，點P為AB邊上一動點（不與點A，B重合），PE⊥OA于點E，PF⊥OB于點F．若AC=20，BD=10，則EF的最小值為（　　）

  A． 2 2

  B． 2 3

  C．4

  D． 2 5
  組卷：1573引用：8難度：0.5

  解析

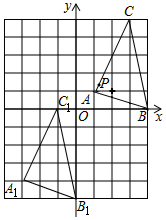• 6．如圖，將正方形網格放置在平面直角坐標系中，其中每個小正方形的邊長均為1，△ABC經過平移后得到△A₁B₁C₁，若AC上一點P（1.2，1.4）平移后對應點為P₁，點P₁繞原點順時針旋轉180°，對應點為P₂，則點P₂的坐標為（　　）

  A．（2.8，3.6）	B．（-2.8，-3.6）
  C．（3.8，2.6）	D．（-3.8，-2.6）
  組卷：1788引用：21難度：0.7

  解析

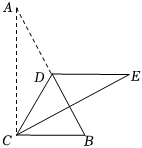• 7．如圖，直角三角形ABC紙片中，∠ACB=90°，點D是AB邊上的中點，連結CD，將△ACD沿CD折疊，點A落在點E處，此時恰好有CE⊥AB．若CB=1，那么CE=

  ．
  組卷：1026引用：5難度：0.4

  解析

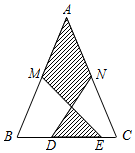• 8．如圖，在△ABC中，AB=AC，M，N分別是AB，AC的中點，D，E為BC上的點，連接DN，EM．若AB=13cm,BC=10cm,DE=5cm,則圖中陰影部分面積為（　　）cm²．

  A．25

  B．35

  C．30

  D．42
  組卷：1190引用：7難度：0.9

  解析

四、解答題

• 23．提出問題：
  在4×4的正方形方格紙上，各個小正方形的頂點稱為格點，以格點為頂點的等腰直角三角形共有幾個？
  問題探究：
  為了解決上面的問題，我們先從最簡單的情形入手，從中找到解決問題的方法．
  探究一：
  如圖1在1×1的正方形方格紙上，以格點為頂點的線段長度可取2個數值：1，

  1

  2

  +

  1

  2

  =

  2

  ，以這些線段組成的等腰直角三角形按三邊長來考慮可以分為以下一種情況：1、1、

  2

  ．
  當斜邊長為

  2

  時，斜邊一定是1×1正方形的對角線，這樣的線段有2條，每條這樣的線段對應著兩個等腰直角三角形，共有2×2=4個．
  故在1×1的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為4個．
  探究二：
  在2×2的正方形方格紙上，以格點為頂點的線段長度可取5個數值：1，2，

  1

  2

  +

  1

  2

  =

  2

  ，

  1

  2

  +

  2

  2

  =

  5

  ，

  2

  2

  +

  2

  2

  =

  2

  2

  ．以這些線段組成的等腰直角三角形按三邊長來考慮可以分為以下三種情況：1、1、

  2

  ；

  2

  、

  2

  、2；2、2、

  2

  2

  ．
  （1）當斜邊長為

  2

  時，斜邊一定是1×1正方形的對角線，這樣的線段有8條，每條這樣的線段對應著兩個等腰直角三角形，共有8×2=16個．
  （2）當斜邊長為2時，圖形中長為2的線段有6條，其中有4條在2×2正方形的四周上，每條這樣的線段對應著一個等腰直角三角形；另有2條在2×2正方形的內部，每條這樣的線段對應著兩個等腰直角三角形，共有4×1+2×2=8個．
  （3）當斜邊長為

  2

  2

  時，斜邊一定是2×2正方形的對角線，這樣的線段有2條，每條這樣的線段對應著兩個等腰直角三角形，共有2×2=4個．
  故在2×2的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為16+8+4=28個．
  探究三：
  如圖2在3×3的正方形方格紙上，以格點為頂點的線段長度可取

  個數值．以這些線段組成的等腰直角三角形按三邊長來考慮可以分為以下五種情況：1、1、

  2

  ；

  2

  、

  2

  、2；2、2、

  2

  2

  ；

  5

  、

  5

  、

  10

  ；3、3、

  3

  2

  ．
  （1）當斜邊長為

  2

  時，斜邊一定是1×1正方形的對角線，這樣的線段有18條，每條這樣的線段對應著兩個等腰直角三角形，共有18×2=36個．
  （2）當斜邊長為2時，圖形中長為2的線段有16條，其中有

  條在3×3正方形的四周上，每條這樣的線段對應著一個等腰直角三角形；另有

  條在3×3正方形的內部，每條這樣的線段對應著兩個等腰直角三角形，共有

  個．
  （3）當斜邊長為

  2

  2

  時，斜邊一定是2×2正方形的對角線，這樣的線段有8條，每條這樣的線段對應著兩個等腰直角三角形，共有8×2=16個．
  （4）當斜邊長為

  10

  時，圖形中長為

  10

  的線段有12條，其中有8條對應著一個等腰直角三角形；
  有4條對應著兩個等腰直角三角形，共有8×1+4×2=16個．
  （5）當斜邊長為

  3

  2

  時，斜邊一定是3×3正方形的對角線，這樣的線段有2條，每條這樣的線段對應著兩個等腰直角三角形，共有2×2=4個．
  故在3×3的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為

  個．
  問題解決：
  如圖3在4×4的正方形方格紙上，以格點為頂點的等腰直角三角形的個數為

  個．
  拓展延伸：
  如圖4在2×2×1的長方體中，以格點為頂點（每個1×1×1小正方體的頂點均為格點），并且以等腰直角三角形為底面的直三棱柱的個數為

  個．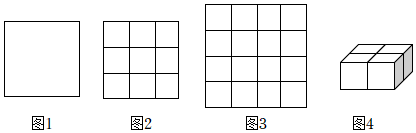
  
  組卷：161引用：2難度：0.3

  解析

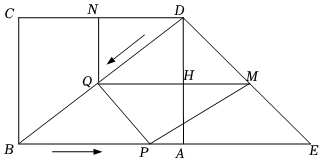• 24．已知：如圖，在矩形ABCD和等腰Rt△ADE中，∠ABD=30°，AE=AD=6

  3

  cm,∠DAE=90°，點P從點B出發，沿BA方向勻速運動，速度為1cm/s；同時，點Q從點D出發，沿DB方向勻速運動，速度為1cm/s.過點Q作QM∥BE，交AD于點H，交DE于點M，過點Q作QN∥BC，交CD于點N．分別連接PQ，PM，設運動時間為t（s）（0＜t＜18），解答下列問題：
  （1）當點P在BD垂直平分線上時，求t的值；
  （2）當PQ⊥BD時，求t的值；
  （3）設五邊形PMDNQ的面積為S（cm²），求S與t之間的函數關系式；
  （4）當PQ=PM時，求t的值．
  組卷：36引用：1難度：0.3

  解析