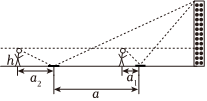
某班課外學習小組利用“鏡面反射法”來測量學校內建筑物的高度．步驟如下：①將鏡子（平面鏡）置于平地上，人后退至從鏡中能看到房頂的位置，測量出人與鏡子的距離；②將鏡子后移，重復①中的操作；③求建筑物高度．如圖所示，前后兩次人與鏡子的距離分別a1m,a2m（a2＞a1），兩次觀測時鏡子間的距離為am,人的“眼高”為hm,則建筑物的高度為（ ）
【考點】解三角形；根據實際問題選擇函數類型．
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/26 8:0:9組卷：107引用：4難度：0.6
相似題
-
1．在①
，②2a-c=2bcosC，③（a-b）（a+b）=（a-c）c這三個條件中任選一個，補充在下面的問題中，并解答該問題．3（a-bcosC）=csinB
在△ABC中，內角A，B，C的對邊分別是a,b,c,且滿足 _____，．b=23
（1）若a+c=4，求△ABC的面積；
（2）求△ABC周長l的取值范圍．發布：2024/12/29 13:0:1組卷：287引用：4難度：0.5 -
2．已知燈塔A在海洋觀察站C的北偏東65°，距離海洋觀察站C的距離為akm,燈塔B在海洋觀察站C的南偏東55°，距離海洋觀察站C的距離為3akm,則燈塔A與燈塔B的距離為（ ）
發布：2024/12/30 4:0:3組卷：50引用：3難度：0.7 -
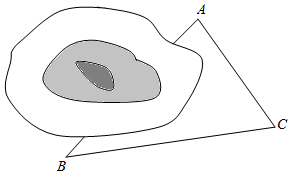3．如圖，在鐵路建設中，需要確定隧道兩端的距離（單位：百米），已測得隧道兩端點A，B到某一點C的距離分別為5和8，∠ACB=60°，則A，B之間的距離為（ ）發布：2024/12/29 13:0:1組卷：295引用：5難度：0.7