2022-2023學(xué)年重慶市康德卷高三（上）一診數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={-1，0，1，2，3}，B={x|x²-x-2＜0}，則A∩B=（　　）

  A．{-1，0，1，2}

  B．{-1，0}

  C．{1，2}

  D．{0，1}
  組卷：5引用：1難度：0.9

  解析

• 2．cos198°cos132°+cos42°sin18°=（　　）

  A． - 3 2

  B． - 1 2

  C． 3 2

  D．1
  組卷：263引用：2難度：0.8

  解析

• 3．設(shè)復(fù)數(shù)z滿足

  z

  i

  +

  z

  ?

  i

  =

  1

  ，則z的虛部為（　　）

  A． - 1 2

  B． 1 2

  C．-1

  D．1
  組卷：14引用：1難度：0.8

  解析

• 4．某人有1990年北京亞運會吉祥物“盼盼”，2008年北京奧運會吉祥物“貝貝”“晶晶”“歡歡”“迎迎”“妮妮”，2010年廣州亞運會吉祥物“阿樣”“阿和”“阿如”“阿意”“樂羊羊”，2022年北京冬奧會吉祥物“冰墩墩”，2022年杭州亞運會吉祥物“琮琮”“蓮蓮”“宸宸”，若他從這15個吉祥物中隨機取出兩個，這兩個吉祥物都是來自在北京舉辦的運動會的概率是（　　）

  A． 1 10

  B． 1 5

  C． 2 5

  D． 2 3
  組卷：47引用：3難度：0.8

  解析

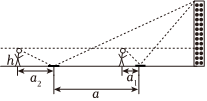• 5．某班課外學(xué)習(xí)小組利用“鏡面反射法”來測量學(xué)校內(nèi)建筑物的高度．步驟如下：①將鏡子（平面鏡）置于平地上，人后退至從鏡中能看到房頂?shù)奈恢茫瑴y量出人與鏡子的距離；②將鏡子后移，重復(fù)①中的操作；③求建筑物高度．如圖所示，前后兩次人與鏡子的距離分別a₁m,a₂m（a₂＞a₁），兩次觀測時鏡子間的距離為am,人的“眼高”為hm,則建筑物的高度為（　　）

  A． ah a 2 - a 1 m

  B． （ a 2 - a 1 ） h a m

  C． a （ a 2 - a 1 ） h m

  D． a h 2 a 2 - a 1 m
  組卷：107引用：4難度：0.6

  解析

• 6．設(shè)等差數(shù)列{a_n}的前n項和為S_n，5S₉=9a₉-36，則a₄=（　　）

  A．-2

  B．-1

  C．1

  D．2
  組卷：24引用：2難度：0.7

  解析

• 7．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的右焦點為F，兩條漸近線分別為l₁，l₂，過F且與l₁平行的直線與雙曲線C及直線l₂依次交于點B，D，點B恰好平分線段FD，則雙曲線C的離心率為（　　）

  A． 4 3

  B． 2

  C． 3

  D．2
  組卷：57引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

• 21．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  2

  2

  ，且過點（2，

  2

  ），點O為坐標(biāo)原點．
  （1）求橢圓C的方程；
  （2）橢圓C上的動點M，P，Q滿足直線MP，MQ的斜率互為相反數(shù)，且點M不在坐標(biāo)軸上，設(shè)直線PQ，OM的斜率分別為k₁，k₂，求k₁k₂的值．
  組卷：32引用：1難度：0.5

  解析

• 22．已知函數(shù)f（x）=ax-lnx,a＞0．
  （1）討論f（x）的零點個數(shù)；
  （2）若對?x∈（0，+∞），不等式e^ax≥ax?f（x）恒成立，求a的取值范圍．
  組卷：37引用：2難度：0.6

  解析