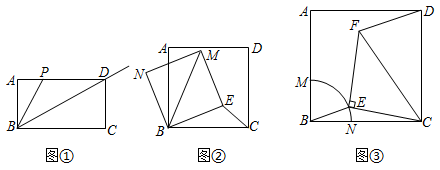
（1）問題提出：如圖①，在矩形ABCD中，AB=1，BC=3，P是AD上一動(dòng)點(diǎn)，則BP+12PD的最小值為33．
（2）問題探究：如圖②，在正方形ABCD中，AB=3，點(diǎn)E是平面上一點(diǎn)，且CE=1，連接BE在BE上方作正方形BEMN，求BM的最大值．
（3）問題解決：為迎接2021年9月在西安舉辦的第14屆全運(yùn)會(huì)，打造體育歷史文化名城，某小區(qū)對(duì)一正方形區(qū)域ABCD進(jìn)行設(shè)計(jì)改造，方便大家鍛煉運(yùn)動(dòng)．如圖③，在正方形內(nèi)設(shè)計(jì)等腰直角△CEF為健身運(yùn)動(dòng)區(qū)域，直角頂點(diǎn)E設(shè)計(jì)在草坪區(qū)域扇形MBN的弧MN上．設(shè)計(jì)鋪設(shè)CF和DF這兩條不同造價(jià)鵝卵石路，已知AB=40米，BM=102，∠CEF=90°，CE=EF，若鋪設(shè)CF路段造價(jià)為每米200元，鋪設(shè)DF路段的造價(jià)為每米100元，請(qǐng)求出鋪設(shè)CF和DF兩條路段的總費(fèi)用的最小值．
3
1
2
3
3
2
【考點(diǎn)】圓的綜合題．
【答案】
3
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/18 11:0:12組卷：161引用：1難度：0.3
相似題
-
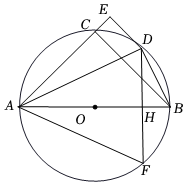1．如圖，Rt△ADE與⊙O交于C、D點(diǎn)，∠AED=90°，AB是⊙O的直徑，AC=BC．過D點(diǎn)作DF⊥AB于H點(diǎn)，交⊙O于F點(diǎn)，連結(jié)AF、BD．
（1）求證：∠ADE=∠EAF；
（2）過點(diǎn)F作FM⊥AD于點(diǎn)M，交AC于點(diǎn)N，連結(jié)DN．若DN∥AB，DM=3，試求出AM的長(zhǎng)度．發(fā)布：2025/5/25 16:30:1組卷：207引用：1難度：0.1 -
2．如圖，已知四邊形ABCD內(nèi)接于⊙O，連接AC、BD，∠ADC+2∠ACD=180°．
（1）求證：BD平分∠ABC；
（2）如圖2，若∠ADB+∠BAC=90°，求證：AB=AC．12
（3）在（2）的條件下，連接DO并延長(zhǎng)交⊙O于點(diǎn)E，交AB、AC于點(diǎn)H、K，連接EB，當(dāng)AC=30，BE=11時(shí)，求tan∠ABC的值．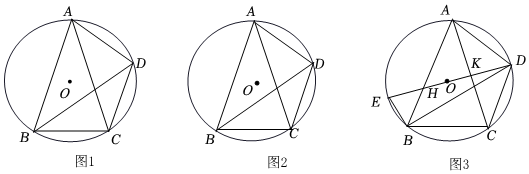
發(fā)布：2025/5/25 15:0:2組卷：245引用：1難度：0.3 -
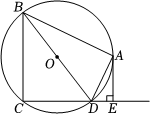3．如圖，四邊形ABCD內(nèi)接于⊙O，BD是⊙O的直徑，AE⊥CD于點(diǎn)E，DA平分∠BDE．
（1）求證：AE是⊙O的切線；
（2）如果AB=4，AE=2，求⊙O的半徑．發(fā)布：2025/5/25 16:0:2組卷：2629引用：23難度：0.7