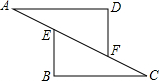
在△AFD和△BEC中，點A、E、F、C在同一直線上，有下面四個論斷：
（1）AD=CB；（2）AE=CF；（3）∠B=∠D；（4）AD∥BC．
請用其中三個作為條件，余下一個作為結論，編一道數學問題，并寫出證明過程．
【考點】全等三角形的判定與性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：320引用：38難度：0.7
相似題
-
1．如圖，在四邊形ABCD中，AD∥BC，∠D=90°，AD=8，BC=6，分別以點A，C為圓心，大于長為半徑作弧，兩弧交于點E，作射線BE交AD于點F，交AC于點O．若點O是AC的中點，則CD的長為 ．12AC發布：2025/5/24 18:0:1組卷：201引用：2難度：0.4 -
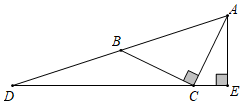2．如圖，△ABC中，∠ACB=90°，AC=BC，點D在AB的延長線上，且BD=AB，連接DC并延長，作AE⊥CD于E，若AE=4，則△BCD的面積為（ ）發布：2025/5/24 18:0:1組卷：651引用：5難度：0.6 -
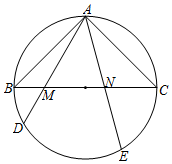3．如圖，BC是半徑為5的圓的直徑，點A是的中點，D，E在另外的半圓上，且?BC=?DE，連接AD，DE分別交直徑BC于點M，N，若CN=2BM，則MN=．?AB發布：2025/5/24 18:0:1組卷：149引用：2難度：0.3