如圖，直線MN的同側放置著角度分別為45°、45°、90°的三角板OAB和角度分別為30°、60°、90°的三角板OCD．點A、O、C在直線MN上，點O、B、D三點共線，OA=OB=OC=3cm.
（1）如圖1，連接BC，則∠BCD=1515°．
（2）如圖2，把三角板OAB向右沿NM方向平移1cm得△AO'B，AB交OD于點G，求四邊形OO'BG的面積．
（3）如圖3，三角板OAB繞著點O旋轉，當AB∥MN時，AB與OD交于點H，在OA上取一點P，∠PHO的角平分線HQ與線段BO的延長線交于點Q，試探索∠AHP與∠HQB的數量關系，并說明理由．
（4）如圖4，若將圖1中的三角板OAB繞著點O以每秒5°的速度順時針旋轉一周，當邊OA或OB與邊CD平行時，求旋轉時間t的值．
【考點】四邊形綜合題．
【答案】15
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/5 8:0:8組卷：25引用：4難度：0.2
相似題
-
1．如圖，四邊形ABCD、EBGF都是正方形．
（1）如圖1，若AB=4，EC=，求FC的長；17
（2）如圖2，正方形EBGF繞點B逆時針旋轉，使點G正好落在EC上，猜想AE、EB、EC之間的數量關系，并證明你的結論；
（3）如圖3，在（2）條件下，∠BCE=22.5°，EC=2，點M為直線BC上一動點，連接EM，過點M作MN⊥EC，垂足為點N，直接寫出EM+MN的最小值．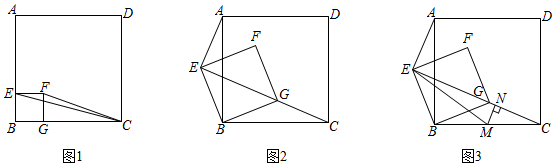
發布：2025/5/24 19:0:1組卷：233引用：2難度：0.5 -
2．如圖1，在菱形ABCD中，AB=10，∠BAD=α（0°＜α＜180°），連接AC，點Q是AD上的一點，連接BQ交AC于點E，過點E作EG⊥AD于點G，連接DE．
（1）當α=60°且時，DQAQ=12=，DG=；DEEQ
（2）當時，若S菱形ABCD=50時．求DG的長度；DQAQ=1
（3）當時，如圖2，分別以點E，A為圓心，大于DQAQ=1為半徑畫弧．交于點F和H，作直線FH，分別交AB，AC，AD于點P，N，M，請你判斷點M的位置是否變化？若不變，求AM的長；若變化說明理由．12AE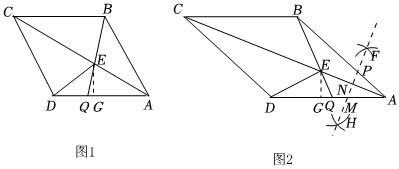
發布：2025/5/24 19:0:1組卷：88引用：4難度：0.3 -
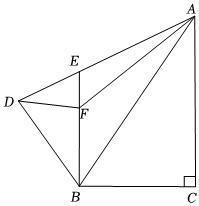3．如圖，在Rt△ABC中，∠ACB=90°，AC=3，BC=，把Rt△ABC沿AB翻折得到Rt△ABD，過點B作BE⊥BC，交AD于點E，點F是線段BE上一點，且tan∠ADF=3．則下列結論中：①AE=BE；②△BED∽△ABC；③BD2=AD?DE；④AF=32．正確的有 .（把所有正確答案的序號都填上）2133發布：2025/5/24 19:30:1組卷：526引用：3難度：0.3