數學課上，劉老師出示了如下框中的題目：
| 如圖，在等邊△ABC中，E為線段AB上一點，D為線段CB延長線上一點，且ED=EC，試確定AE與DB的大小關系，并說明理由． |
|
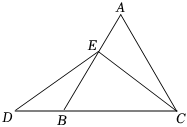
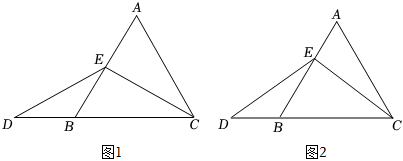
（1）特殊情況?探索結論
當點E為線段AB的中點時，如圖1，確定線段AE與DB的大小關系請你直接寫出結論：AE
=
=
DB．（選填“＞”，“＜”或“=”）（2）特例啟發?解答題目
當E為線段AB上除中點外的任意一點時，其余條件不變，如圖2，（1）中線段AE與DB的大小關系會發生改變嗎？若不會，請證明；若改變，請說明理由．
（3）拓展結論?設計新題
經過以上的解答，小聰和小明發現如果把劉老師的題目稍加改變，就會得到這樣一道題目：在等邊△ABC中，點E在直線AB上，點D在直線BC上，且ED=EC．若△ABC的邊長為1，AE=2，求CD的長．
請你根據（1）（2）的探究過程，嘗試解決兩人改編的此問題，直接寫出CD的長．
【考點】三角形綜合題．
【答案】=
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 13:30:5組卷：223引用：5難度：0.1
相似題
-
1．如圖1，在△ABC中，AB=AC，點D是BC的中點，點E在AD上，連接BE、CE．
（1）求證：BE=CE；
（2）如圖2，若BE的延長線交AC于點F，且BF⊥AC，垂足為F，原題設其它條件不變．求證：∠CAD=∠CBF．
（3）在（2）的條件下，若∠BAC=45°，判斷△CFE的形狀，并說明理由．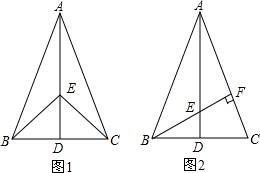
發布：2025/6/3 10:30:2組卷：365引用：4難度：0.3 -
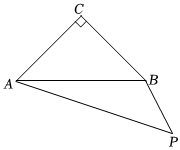2．如圖，在△ABC中，AC=BC，∠ACB=90°，∠APB=45°，連接CP，將線段CP繞點C順時針旋轉90°得到線段CQ，連接AQ．
（1）依題意，補全圖形，并證明：AQ=BP；
（2）求∠QAP的度數；
（3）若N為線段AB的中點，連接NP，請用等式表示線段NP與CP之間的數量關系，并證明．發布：2025/6/3 11:0:2組卷：485引用：6難度：0.1 -
3．已知，在△ABC中，∠ACB=90°，AC=8，tanA=
，D是斜邊AB上一點，連接CD．34
（1）當D是AB的中點時．
①如圖①，求CD的長；
②如圖②，過點D作AB的垂線交AC于點E，求DE的長；
③如圖③，過點A作CD的垂線，交CD的延長線于點M，求sin∠DAM的值；
（2）將△ACD沿直線CD翻折，使得點A落在同一平面內的點A′處，當A′D∥BC時，求AD的長．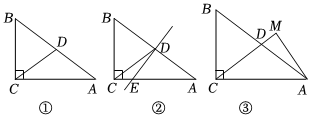
發布：2025/6/3 11:30:1組卷：55引用：2難度：0.4