折紙是我國傳統的民間藝術，通過折紙不僅可以得到許多美麗的圖形，折紙的過程還蘊含著豐富的數學知識，在綜合與實踐課上，老師讓同學們以“正方形的折疊”為主題開展了數學活動．
（1）操作判斷：
在AD上選一點P，沿BP折疊，使點A落在正方形內部的點M處，把紙片展平，過M作EF∥BC交AB、CD、BP于點E、F、N，連接PM并延長交CD于點Q，連接BQ，如圖①，當E為AB中點時，△PMN是 等邊等邊三角形．
（2）遷移探究：
如圖②，若BE=5，且ME?MF=10，求正方形ABCD的邊長．
（3）拓展應用：
如圖③，若MNBC=1n（n＞1），直接寫出CQBC的值為 n-1n+1n-1n+1．
MN
BC
=
1
n
CQ
BC
n
-
1
n
+
1
n
-
1
n
+
1
【考點】相似形綜合題．
【答案】等邊；
n
-
1
n
+
1
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/22 7:0:2組卷：2085引用：6難度：0.3
相似題
-
1．如圖1，在Rt△ABC中，∠BAC=90°，D為邊AB上一點，∠ACD=∠B．
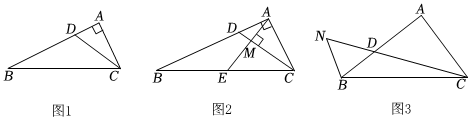
（1）求證：AC2=AD?AB；
（2）如圖2，過點A作AM⊥CD于M，交BC于點E，若AB=4AD，求的值；AMME
（3）如圖，N為CD延長線上一點，連接BN，且∠NBD=2∠ACD，若，直接寫出tan∠ACD=1n（n＞1）的值（用含n的代數式表示）．NDDC發布：2025/5/22 10:30:1組卷：557引用：4難度：0.1 -
2．如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=3．點D是邊AC上一動點（不與A、C重合），聯結BD，過點C作CF⊥BD，分別交BD、AB于點E、F．
（1）當CD=2時，求∠ACF的正切值；
（2）設CD=x,，求y關于x的函數解析式，并寫出x的定義域；AFBF=y
（3）聯結FD并延長，與邊BC的延長線相交于點G，若△DGC與△BAC相似，求的值．AFBF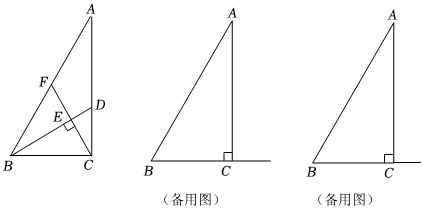
發布：2025/5/22 11:30:2組卷：530引用：1難度：0.4 -
3．【問題提出】
在一次折紙活動課上，老師提出這樣一個問題：如何把一張正方形的紙通過折疊的方式等分成若干份？
【解決問題】
以下是某個小組的活動過程：若是等分成兩份，如圖①直接對折，四等分、八等分在二等分的基礎上進行對折即可，那三等分呢？
學習過相似三角形的相關知識后，小明提出了如下方法：如圖②，折出AD、BC的中點E、F，連接AF、CE交對角線BD于點G、H，過點G、H折出AB、CD的平行線，折痕MN、PQ三等分正方形紙片．
（1）小明的想法正確嗎？若正確，請證明：
【類比學習】
（2）尺規作圖：如圖③，請你用尺規作圖，作線段AB的三等分點．（保留作圖痕跡，并簡要說明作法）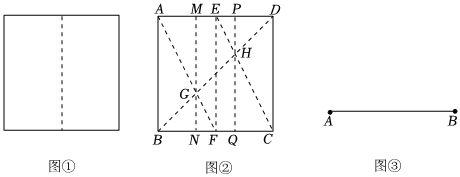
發布：2025/5/22 14:0:1組卷：248引用：3難度：0.4