試探究以下問題：平面上有n（n≥3）個點，任意三個點不在同一直線上，過任意三點作三角形，一共能作出多少不同的三角形？
（1）分析：當僅有3個點時，可作多少個三角形？當有4個點時，可作多少個三角形？當有5個點時，可作多少個三角形？
（2）歸納：考查點的個數n和可作出的三角形的個數Sn．
【考點】規律型：數字的變化類．
【答案】（1）1，4，10；
（2）．
（2）
n
（
n
-
1
）
（
n
-
2
）
6
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：9引用：1難度：0.5
相似題
-
1．已知：a是不為1的有理數，我們把
稱為a的差倒數．如：5的差倒數是11-a，-3的差倒數是11-5=-14，已知11-（-3）=14，a2是a1的差倒數，a3是a2的差倒數，a4是a3的差倒數，…，以此類推，a2020的值為（ ）a1=32發布：2025/6/21 13:0:29組卷：104引用：3難度：0.6 -
2．觀察下列單項式：-x,3x2，-5x3，7x4，…，-37x19，39x20，…．
（1）這組單項式的系數的符號規律是 ，系數的絕對值規律是 ；
（2）這組單項式的次數的規律是 ；
（3）根據上面的歸納，可以猜想第n個單項式是（只能填寫一個代數式） ；
（4）請你根據猜想，寫出第2008個、第2009個單項式，它們分別是 ，．發布：2025/6/21 19:30:1組卷：111引用：1難度：0.6 -
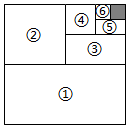3．如圖，將一個邊長為1的正方形紙片分割成7個部分，部分1是邊長為1的正方形紙片面積的一半，部分2是部分1面積的一半，部分3是部分2面積的一半，依此類推．陰影部分的面積是 ；受此啟發，則+12+14+…+18的值為 ．126發布：2025/6/21 12:0:1組卷：974引用：3難度：0.8