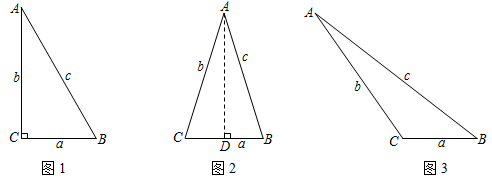
在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如圖1,則有a2+b2=c2;若△ABC為銳角三角形,小明猜想:a2+b2>c2.理由如下:
如圖2,過點A作AD⊥CB于點D,設CD=x.
在Rt△ADC中,AD2=b2-x2;
在Rt△ADB中,AD2=c2-(a-x)2.
∴b2-x2=c2-(a-x)2,即a2+b2=c2+2ax.
∵a>0,x>0,
∴2ax>0,
∴a2+b2>c2.
故當△ABC為銳角三角形時,a2+b2>c2.
∴小明的猜想是正確的.
請你猜想,當△ABC為鈍角三角形時,如圖3,a2+b2與c2的大小關系,并證明你猜想的結論.
【考點】勾股定理.
【答案】a2+b2<c2,證明見解答.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/17 8:30:1組卷:156引用:1難度:0.5



