我們學(xué)習(xí)了圖形的三大變換：平移、旋轉(zhuǎn)與翻折．這些變換在探索與發(fā)現(xiàn)圖形的性質(zhì)及圖形關(guān)系等方面有著廣泛的應(yīng)用請利用圖形變換知識解決下列問題：
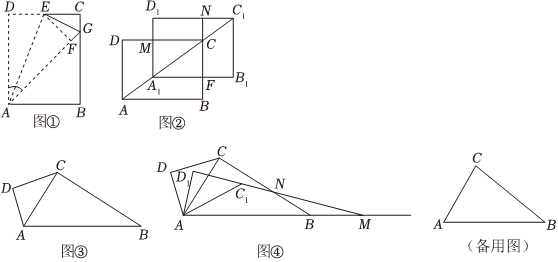
（1）翻折：如圖①，在矩形ABCD中，點E是邊CD的中點，將△ADE沿AE折疊后得到△AFE，且點F在矩形ABCD內(nèi)部．將AF延長交邊BC于點G．若CGGB=15，則ADAB=6262；
（2）平移．如圖②，矩形ABCD中，AB=20，AD=15，將矩形ABCD沿對角線AC方向平移得到矩形A1B1C1D1，平移的速度為5個單位/秒，設(shè)平移的時間為t秒（0＜t＜5），記圖中矩形MCND1的面積為S，求S與t之間的函數(shù)關(guān)系式，并求S的最大值；
（3）旋轉(zhuǎn)；如圖③，已知Rt△ADC∽Rt△ACB，其中∠D=∠ACB=90°，AB=25，AC=15，現(xiàn)將Rt△ADC繞著A點順時針方向旋轉(zhuǎn)α角度（0°＜α＜180°）得到Rt△AD1C1，如圖④，直線D1C1分別與直線AB、BC交于點M、N．在Rt△ADC繞著A點旋轉(zhuǎn)的過程中，探究．當BM=25-310或910-25或1258或1025-310或910-25或1258或10時，△BMN是等腰三角形（直接寫結(jié)果）．
CG
GB
=
1
5
AD
AB
6
2
6
2
25
-
3
10
9
10
-
25
125
8
25
-
3
10
9
10
-
25
125
8
【考點】相似形綜合題．
【答案】；或或或10
6
2
25
-
3
10
9
10
-
25
125
8
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/21 12:0:1組卷：69引用：2難度：0.5
相似題
-
1．圖①、圖②、圖③都是5×4的正方形網(wǎng)格，每個小正方形的頂點稱為格點，每個小正方形的邊長為1，點A、B、C、D均在格點上．請按要求解答問題．（畫圖只能用無刻度的直尺，保留作圖痕跡）
要求：（1）如圖①，=；BECE
（2）如圖②，在BC上找一點F使BF=2；
（3）如圖③，在AC上找一點M，連結(jié)BM、DM，使△ABM∽△CDM．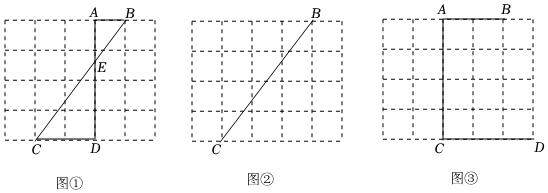
發(fā)布：2025/6/7 8:30:2組卷：210引用：4難度：0.5 -
2．小波在復(fù)習(xí)時，遇到一個課本上的問題，溫故后進行了操作、推理與拓展．
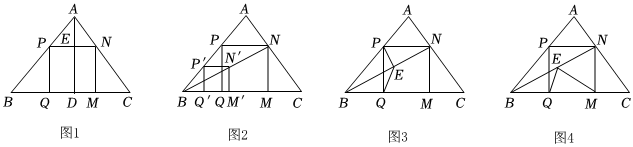
（1）溫故：如圖1，在△ABC中，AD⊥BC于點D，正方形PQMN的邊QM在BC上，頂點P，N分別在AB，AC上，且．若BC=6，AD=4，則正方形PQMN的邊長等于 ；PNBC+MNAD=1
（2）操作：能畫出這類正方形嗎？小波按數(shù)學(xué)家波利亞在《怎樣解題》中的方法進行操作：如圖2，任意畫△ABC，在AB上任取一點P'，畫正方形P'Q'M'N'，使Q'，M'在BC邊上，N'在△ABC內(nèi)，連結(jié)BN'并延長交AC于點N，畫NM⊥BC于點M，NP⊥NM交AB于點P，PQ⊥BC于點Q，得到四邊形PQMN；
（3）推理：如圖3，若點E是BN的中點，求證：EP=EQ；
（4）拓展：在（2）的條件下，射線BN上截取NE=NM，連結(jié)EQ，EM（如圖4）．當∠NBM=30°時，猜想∠QEM的度數(shù)，并嘗試證明．
請幫助小波解決“溫故”、“推理”、“拓展”中的問題．發(fā)布：2025/6/7 9:0:2組卷：103引用：3難度：0.3 -
3．感知：如圖①，在四邊形ABCD中，AB∥CD，∠B=90°，點P在BC邊上，當∠APD=90°時，△ABP與△PCD是否相似？（填“是”或“否”）．
探究：如圖②，在四邊形ABCD中，點P在BC邊上，當∠B=∠C=∠APD時，求證：△ABP∽△PCD．
拓展：如圖③，在△ABC中，點P是邊BC的中點，點 D、E分別在邊AB、AC上．若∠B=∠C=∠DPE=45°，
BC=，CE=9，則DE的長為 ．122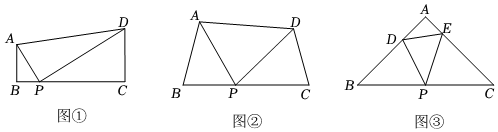
發(fā)布：2025/6/7 5:0:1組卷：395引用：5難度：0.4