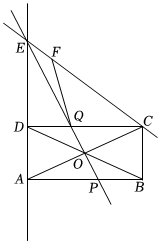
如圖，在矩形ABCD中，AB=12，O是對角線AC，BD的交點，點P是線段AB上的動點，直線PO交直線AD于點E，交CD于點Q，連接CE，在直線CE上取點F，使FQ=CQ（點F不與點C重合）．
（1）當點D是線段AE的中點時，求DQCQ的值．
（2）若點F與點E重合時，AP=9，求AD的長．
（3）已知AD=5．在點P的移動過程中，是否存在某一位置，使得FQ與△ABD的某一邊平行？若存在，求AP的長；若不存在，請說明理由．
DQ
CQ
【考點】相似形綜合題．
【答案】（1）；
（2）；
（3）或或或或12．
1
2
（2）
12
2
（3）
204
29
444
49
84
19
132
23
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/8 8:0:8組卷：94引用：3難度：0.5
相似題
-
1．如圖，點O為矩形ABCD的對稱中心，AB=10cm,BC=12cm,點E、F、G分別從A、B、C三點同時出發，沿矩形的邊按逆時針方向勻速運動，點E的運動速度為1cm/s,點F的運動速度為3cm/s,點G的運動速度為1.5cm/s,當點F到達點C（即點F與點C重合）時，三個點隨之停止運動．在運動過程中，△EBF關于直線EF的對稱圖形是△EB′F．設點E、F、G運動的時間為t（單位：s）．
（1）當t=s時，四邊形EBFB′為正方形；
（2）若以點E、B、F為頂點的三角形與以點F，C，G為頂點的三角形相似，求t的值；
（3）是否存在實數t,使得點B′與點O重合？若存在，求出t的值；若不存在，請說明理由．
發布：2025/6/1 23:30:1組卷：2613引用：19難度：0.3 -
2．如圖（1），在四邊形ABCD中，AB∥DC，CB⊥AB，AB=14cm,BC=CD=6cm,動點P從點D開始沿DA邊勻速運動，動點Q從點A開始沿AB邊勻速運動，它們的運動速度均為1cm/s.點P和點Q同時出發，設運動的時間為t（s），0＜t＜10．
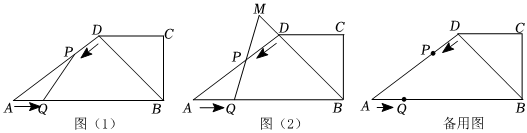
（1）用含t的代數式表示AP；
（2）當以點A、P、Q為頂點的三角形與△ABD相似時，求t的值；
（3）如圖（2），延長QP、BD，兩延長線相交于點M，當△QMB為直角三角形時，直接寫出t的值．發布：2025/6/1 23:30:1組卷：220引用：3難度：0.3 -
3．【教材呈現】如圖是華師版九年級上冊數學教材第98頁的部分內容．
如圖（1），先把一張矩形紙片ABCD上下對折．設折痕為MN；如圖（2），再把點B疊在折痕線上，得到△ABE．過點B向右折紙片，使D、Q、A三點仍保持在一條直線上，得折痕PQ．
（1）求證：△PBE∽△QAB．
（2）你認為△PBE和△BAE相似嗎？如果相似，給出證明；如果不相似，請說明理由．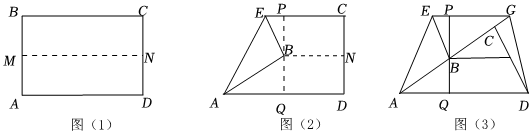
【問題解決】
（1）對教材中的第一問寫出證明過程．
（2）你認為△PBE和△BAE相似嗎？如果相似，給出證明；如果不相似，請說明理由．
【結論應用】在圖（2）的基礎上，將紙片ABCD按圖（3）所示翻折，恰好點C落在直線AB上，得到△CDG．若AB=2，則BC的長為 ．發布：2025/6/2 0:30:1組卷：182引用：1難度：0.4