折紙,操作簡單,富有數學趣味,常常能為證明一個命題提供思路和方法.
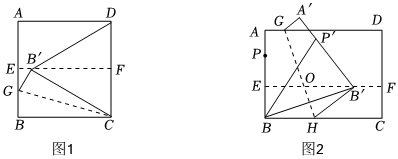
【動手操作】如圖1,把正方形紙片ABCD對折后再展開,折痕為EF;將點B翻折到EF上點B′,折痕為CG;連接B′D.
(1)判斷△B′CD的形狀并說明理由;
【類比操作】如圖2,點P為長方形紙片ABCD的邊AB上一點,折疊紙片,使B與P兩點重合,展平紙片,得到折痕EF;折疊紙片,使點B折疊后落在EF上的點B處,展平紙片,得到折痕GH、EF與GH交于點O;連接BP′、BB′.
(2)求證:點O在BP′的垂直平分線上;
(3)試探究∠P′BB′與∠CBB′之間的數量關系,并說明理由.
【考點】四邊形綜合題.
【答案】(1)△B′CD是等邊三角形,理由見解答;
(2)證明過程見解答;
(3)∠P′BB′=2∠CBB′,理由見解答.
(2)證明過程見解答;
(3)∠P′BB′=2∠CBB′,理由見解答.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/10/7 6:0:2組卷:207引用:1難度:0.1
相似題
-
1.如圖1和圖2,在四邊形ABCD中,AB=CD=6,AD=2,BC=8,∠B=∠C=60°,點K在CD邊上,點M,N分別在AB,BC邊上,且AM=CN=2,點P從點M出發沿折線MB-BN勻速運動,點E在CD邊所在直線上隨P移動,且始終保持∠MPE=∠B;點Q從點D出發沿DC勻速運動,點P,Q同時出發,點Q的速度是點P的一半,點P到達點N停止,點Q隨之停止.設點P移動的路程為x.

(1)當x=5時,求PN的長;
(2)當MP⊥BC時,求x的值;
(3)用含x的式子表示QE的長;
(4)已知點P從點M到點B再到點N共用時20秒,若,請直接寫出點K在線段QE上(包括端點)的總時長.CK=154發布:2025/5/22 10:30:1組卷:224引用:2難度:0.1 -
2.定義:我們把對角線相等的凸四邊形叫做“等角線四邊形”.

(1)在已經學過的“①平行四邊形;②矩形;③菱形;④正方形“中,一定是“等角線四邊形”的是 (填序號);
(2)如圖1,在正方形ABCD中,點E,F分別在邊BC,CD上,且EC=DF,連接EF,AF,求證:四邊形ABEF是等角線四邊形;
(3)如圖2,△ABC中,∠ABC=90°,AB=4,BC=3,D為線段AB的垂直平分線上一點,若以點A,B,C,D為頂點的四邊形是等角線四邊形,求這個等角線四邊形的面積.發布:2025/5/22 9:0:1組卷:478引用:1難度:0.3 -
3.在數學興趣小組活動中,同學們對矩形的折疊問題進行了探究.在矩形ABCD中,AB=6,AD=3,E是AB邊上一點,AE=2,F是直線CD上一動點,以直線EF為對稱軸,點A關于直線EF的對稱點為A'.

(1)如圖(1),求四邊形AEA'F的面積.
(2)如圖(2),連接CE,當點A'落在直線CE上時,求tan∠CFA'的值.
(3)當點F,A',B三點在一條直線上時,則DF的長度為 .發布:2025/5/22 9:0:1組卷:225引用:1難度:0.1


