如圖，在△ABC中，AD是BC邊上的中線，交BC于點(diǎn)D．
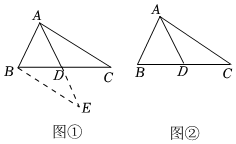
（1）如圖①，延長(zhǎng)AD到點(diǎn)E，使DE=AD，連接BE．求證：△ACD≌△EBD；
（2）若AB=6，AC=8，則中線AD的取值范圍是多少？請(qǐng)說(shuō)明理由．
【考點(diǎn)】全等三角形的判定與性質(zhì)；三角形三邊關(guān)系．
【答案】（1）證明見(jiàn)解析；
（2）1＜AD＜7，理由見(jiàn)解析．
（2）1＜AD＜7，理由見(jiàn)解析．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/26 4:0:1組卷：45引用：2難度：0.5
相似題
-
1．已知四邊形ABCD中，∠A=∠C=90°，AB=BC，∠ABC=120°，∠MBN=60°，∠MBN繞B點(diǎn)旋轉(zhuǎn)，它的兩邊分別交AD，DC（或它們的延長(zhǎng)線）于E，F(xiàn)．
當(dāng)∠MBN繞B點(diǎn)旋轉(zhuǎn)到AE=CF時(shí)（如圖1），易證AE+CF=EF；
當(dāng)∠MBN繞B點(diǎn)旋轉(zhuǎn)到AE≠CF時(shí)，在圖2和圖3這兩種情況下，上述結(jié)論是否成立？若成立，請(qǐng)給予證明；若不成立，線段AE，CF，EF又有怎樣的數(shù)量關(guān)系？請(qǐng)寫出你的猜想，不需證明．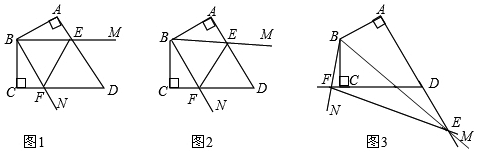
發(fā)布：2025/5/28 3:0:1組卷：6615引用：37難度：0.1 -
2．如圖，在△ABC中，∠BAC=90°，AB=AC，BE平分∠ABC，CE⊥BE．求證：BD=2CE．發(fā)布：2025/5/28 3:30:1組卷：553引用：5難度：0.5 -
3．如圖所示，已知點(diǎn)E、F在直角三角形ABC的邊AB所在的直線上，且AE=BF，F(xiàn)H∥EG∥AC，F(xiàn)H、EG分別交邊BC所在的直線于點(diǎn)H、G．
（1）如圖（1），如果點(diǎn)E、F在邊AB上，那么線段EG、FH、AC的長(zhǎng)度關(guān)系為．
（2）如圖（2），如果點(diǎn)E在邊AB上，點(diǎn)F在AB的延長(zhǎng)線上，那么線段EG、FH、AC的長(zhǎng)度關(guān)系為．
（3）如圖（3），如果點(diǎn)E在邊AB的反向延長(zhǎng)線上，點(diǎn)F在AB的延長(zhǎng)線上，那么線段EG、FH、AC的長(zhǎng)度關(guān)系為．
對(duì)（1）（2）（3）三種情況的結(jié)論，請(qǐng)任選一個(gè)給予說(shuō)明．
發(fā)布：2025/5/28 3:0:1組卷：137引用：1難度：0.5