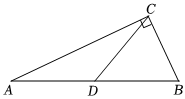
如圖，已知Rt△ABC中，∠ACB=90°，D為斜邊AB的中點，連接CD．過C點作CD的垂線，并在這條線上（C的下方）截取CE=2CD，連接BE．
（1）根據(jù)題目條件補全圖形；
（2）證明：∠A=∠BCE；
（3）用等式表示AC、BC和BE的數(shù)量關系，并證明．
【考點】三角形綜合題．
【答案】（1）見解析；
（2）見解析；
（3），證明見解析．
（2）見解析；
（3）
AC
=
BC
+
B
E
2
-
B
C
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：169引用：4難度：0.2
相似題
-
1．【問題呈現(xiàn)】某學校的數(shù)學社團成員在學習時遇到這樣一個題目：
如圖1，在△ABC中，AB＞AC，AD平分∠BAC交BC于點D，點E在DC的延長線上，過E作EF∥AB交AC的延長線于點F，當BD：DE=1時，試說明：AF+EF=AB；
【方法探究】
社團成員在研究探討后，提出了下面的思路：
在圖1中，延長線段AD，交線段EF的延長線于點M，可以用AAS明△ABD≌△MED，從而得到EM=AB…
（1）請接著完成剩下的說理過程；
【方法運用】
（2）在圖1中，若BD：DE=k,則線段AF、EF、AB之間的數(shù)量關系為 （用含k的式子表示，不需要證明）；
（3）如圖2，若AB=7，EF=6，AF=8，BE=12，求出BD的長；
【拓展提升】
（4）如圖3，若DE=2BD，連接AE，已知AB=9，tan∠DAF=，AE=212，且AF＞EF，則邊EF的長=．17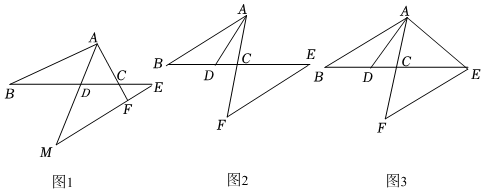
發(fā)布：2025/5/25 0:0:2組卷：320引用：4難度：0.2 -
2．（1）感知：如圖①．AB=AD，AB⊥AD，BF⊥AF于點F，DG⊥AF于點G．求證：△ADG≌△BAF；
（2）拓展：如圖②，點B，C在∠MAN的邊AM，AN上，點E，F(xiàn)在∠MAN在內(nèi)部的射線AD上，∠1，∠2分別是△ABE，△CAF的外角，已知AB=AC，∠1=∠2=∠BAC．求證：△ABE≌△CAF；
（3）應用：如圖③，在△ABC中，AB=AC，AB＞BC，點在D邊BC上，CD=2BD，點E，F(xiàn)在線段AD上，∠1=∠2=∠BAC．若△ABC的面積為12，則△ABE與△CDF的面積之和為．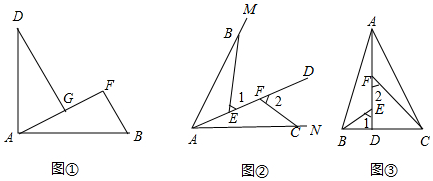
發(fā)布：2025/5/24 23:0:1組卷：156引用：2難度：0.3 -
3．在△ABC中，AB=BC，∠B=45°，AD為BC邊上的高，M為線段AB上一動點．
（1）如圖1，連接CM交AD于Q，若∠ACM=45°，AB=．求線段DQ的長度；2
（2）如圖2，點M，N在線段AB上，且AM=BN，連接CM，CN分別交線段AD于點Q、P，若點P為線段CN的中點，求證：AQ+CD=AB；2
（3）如圖3，若AD=4，當點M在運動過程中，射線DB上有一點G，滿足BM=10DG，AG+2MG的最小值．55
發(fā)布：2025/5/24 23:0:1組卷：102引用：1難度：0.1