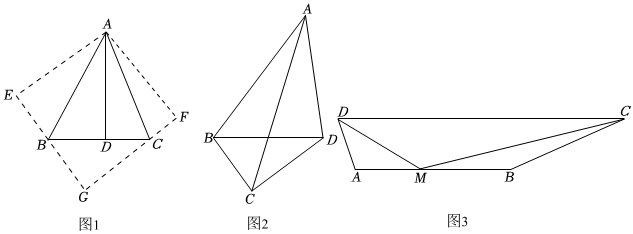
【問題情境】如圖1，在△ABC中，∠BAC=45°，AD⊥BC于點D，BD=6，DC=4，求AD的長．
【問題解決】小明同學是這樣分析的：將△ABD沿著AB翻折得到△ABE，將△ACD 沿著AC翻折得到△ACF，延長EB、FC相交于點G．請按著小明的思路解答下列問題：
（1）說明四邊形AEGF是正方形；
（2）在Rt△GBC中運用勾股定理，求出AD的長．
【方法提煉】通過問題解決，小明發現翻折是解決問題的有效辦法之一，它可以將問題中的相關信息有效地集中、關聯與重組．請根據自己理解，解答下列問題：
（3）如圖2，四邊形ABCD中，∠BAD=45°，∠BCD=90°，BC=6，CD=8，求AC的最大值．
（4）如圖3，四邊形ABCD中，BC=6，AD=2，點M是AB上一點，且∠DMC=135°，AM=3，BM=4，則CD的最大值為 1313.（直接寫出結果）?
【考點】四邊形綜合題．
【答案】13
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/27 8:0:10組卷：198引用：2難度：0.1
相似題
-
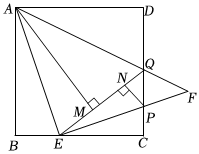1．已知四邊形ABCD是邊長為1的正方形，點E是邊BC上的動點，以AE為直角邊在直線BC的上方作等腰直角三角形AEF，∠AEF=90°，EF、AF與CD分別相交于點P、Q，連接EQ，過點A作AM⊥EQ，垂足為點M，過點P作PN⊥EQ，垂足為點N，設BE=m.
（1）求AM的長；
（2）用含有m的代數式表示CQ；
（3）用含有m的代數式表示PN，并求PN的最大值．發布：2025/5/23 19:30:1組卷：224引用：1難度：0.3 -
2．綜合與探究
問題提出：某興趣小組在綜合與實踐活動中提出這樣一個問題：在等腰直角三角板ABC中，∠BAC=90°，AB=AC，D為BC的中點，用兩根小木棒構建角，將頂點放置于點D上，得到∠MDN，將∠MDN繞點D旋轉，射線DM，DN分別與邊AB，AC交于E，F兩點，如圖1所示．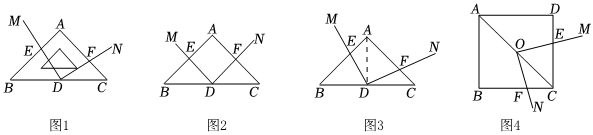
（1）操作發現：如圖2，當E，F分別是AB，AC的中點時，試猜想線段DE與DF的數量關系是 ；
（2）類比探究：如圖3，當E，F不是AB，AC的中點，但滿足BE=AF時，求證△BED≌△AFD；
（3）拓展應用：如圖4，將兩根小木棒構建的角，放置于邊長為4的正方形紙板上，頂點和正方形對角線AC的中點O重合，射線OM，ON分別與DC，BC交于E，F兩點，且滿足DE=CF，請求出四邊形OFCE的面積．發布：2025/5/23 19:30:1組卷：247引用：5難度：0.4 -
3．新定義：垂直于圖形的一邊且等分這個圖形面積的直線叫作圖形的等積垂分線，等積垂分線被該圖形截的線段叫做等積垂分線段．
問題探究：
（1）如圖1，等邊△ABC邊長為3，垂直于BC邊的等積垂分線段長度為 ；
（2）如圖2，在△ABC中，AB=8，，∠B=30°，求垂直于BC邊的等積垂分線段長度；BC=63
（3）如圖3，在四邊形ABCD中，∠A=∠C=90°，AB=BC=6，AD=3，求出它的等積垂分線段長．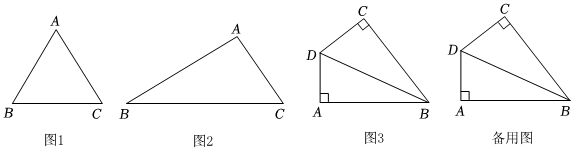
發布：2025/5/23 19:30:1組卷：398引用：2難度：0.2