設二次函數y=ax2+bx+1與x軸的交點為（x1，0）（x2，0），若b＞0且y的最小值為1-a.
（1）x1+x2=-2-2；
（2）當2≤x≤4時，不等式y＞（2a+4）x-2恒成立，則實數a的取值范圍為 a＞54a＞54．
5
4
5
4
【考點】二次函數與不等式（組）；二次函數的最值．
【答案】-2；a＞
5
4
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 18:0:1組卷：149引用：1難度：0.4
相似題
-
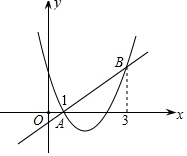1．如圖，直線y=x+m和拋物線y=x2+bx+c都經過點A（1，0），B（3，2）．
（1）求m的值和拋物線的關系式；
（2）求不等式x2+bx+c＞x+m的解集（直接寫出答案）．發布：2025/5/24 17:0:2組卷：772引用：15難度：0.5 -
2．如圖所示，已知二次函數y1=ax2+bx+c（a≠0）與一次函數y2=kx+b（k≠0）的圖象相交于點A（-2，4），B（8，2），則能使y1＞y2成立的x的取值范圍是 ．發布：2025/5/24 17:30:1組卷：100引用：2難度：0.7 -
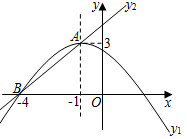3．如圖，拋物線y1=ax2+bx+c（a≠0）的頂點坐標A（-1，3），與x軸的一個交點B（-4，0），直線y2=mx+n（m≠0）與拋物線交于A、B兩點，下列結論：①2a-b=0；②拋物線與x軸的另一個交點坐標是（2，0）；③7a+c＞0；④方程ax2+bx+c-2=0有兩個不相等的實數根；⑤當-4＜x＜-1時，則y2＜y1．其中正確結論的個數為（ ）發布：2025/5/24 9:0:1組卷：1712引用：7難度：0.4