已知圓C1經過兩點E（-4，-2），F（-6，0），且圓心C1在直線l：2x-y+8=0上．
（1）求圓C1的方程；
（2）求過點G（-6，3）且與圓C1相切的直線方程；
（3）設圓C1與x軸相交于A、B兩點，點P為圓C1上不同于A、B的任意一點，直線PA、PB交y軸于M、N點．當點P變化時，以MN為直徑的圓C2是否經過圓C1內一定點？請證明你的結論．
【考點】直線和圓的方程的應用．
【答案】（1）（x+4）2+y2=4；
（2）5x+12y-6=0和x=-6；
（3）經過；
證明：設P（x0，y0），則，
由圓C1的方程，
令y=0，可得A（-6，0），B（-2，0），
∴直線PA的方程為，
進而得，
同法得，
∴圓C2的圓心，
半徑=，
∴圓C2的方程為：，
整理得，
由y=0得x=，
而點在圓C1內，
故圓C2過圓C1內定點（-2，0）．
（2）5x+12y-6=0和x=-6；
（3）經過；
證明：設P（x0，y0），則
（
x
0
+
4
）
2
+
y
0
2
=
4
由圓C1的方程，
令y=0，可得A（-6，0），B（-2，0），
∴直線PA的方程為
y
=
y
0
x
0
+
6
（
x
+
6
）
進而得
M
（
0
，
6
y
0
x
0
+
6
）
同法得
N
（
0
，
2
y
0
x
0
+
2
）
∴圓C2的圓心
C
2
（
0
，
6
y
0
x
0
+
6
+
2
y
0
x
0
+
2
2
）
半徑
r
2
2
（
6
y
0
x
0
+
6
-
2
y
0
x
0
+
2
2
）
2
∴圓C2的方程為：
x
2
+
（
y
-
6
y
0
x
0
+
6
+
2
y
0
x
0
+
2
2
）
2
=
（
6
y
0
x
0
+
6
-
2
y
0
x
0
+
2
2
）
2
整理得
x
2
+
y
2
-
（
6
y
0
x
0
+
6
+
2
y
0
x
0
+
2
）
y
-
12
=
0
由y=0得x=
±
2
3
而點
（
-
2
3
，
0
）
故圓C2過圓C1內定點（-2
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：156引用：2難度：0.4
相似題
-
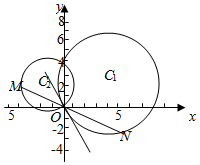1．已知圓C1：（x-4）2+（y-2）2=20與y軸交于O，A兩點，圓C2過O，A兩點，且直線C2O與圓C1相切；
（1）求圓C2的方程；
（2）若圓C2上一動點M，直線MO與圓C1的另一交點為N，在平面內是否存在定點P使得PM=PN始終成立，若存在求出定點坐標，若不存在，說明理由．發布：2024/10/16 15:0:1組卷：547引用：7難度：0.3 -
2．若直線ax+y=0始終平分圓x2+y2-2ax+2ay+2a2+a-1=0的周長，則a的值為（ ）
發布：2024/12/8 10:30:3組卷：358引用：2難度：0.8 -
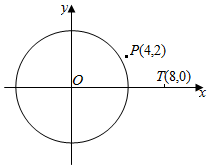3．已知直角坐標系xOy中，圓O：x2+y2=16．
①過點P（4，2）作圓O的切線m,求m的方程；
②直線l：y=kx+b與圓O交于點M，N兩點，已知T（8，0），若x軸平分∠MTN，證明：不論k取何值，直線l與x軸的交點為定點，并求出此定點坐標．發布：2024/9/25 3:0:1組卷：148引用：2難度：0.6