小明想知道一堵墻上點A的高度（AO⊥OD），但又沒有直接測量的工具，于是設計了下面的方案，請你先補全方案，再說明理由．
第一步：找一根長度大于OA的直桿，使直桿靠在墻上，且頂端與點A重合，記下直桿與地面的夾角∠ABO；
第二步：使直桿頂端豎直緩慢下滑，直到∠OCDOCD=∠ABOABO．標記此時直桿的底端點D；
第三步：測量ODOD的長度，即為點A的高度．
說明理由；
【考點】全等三角形的應用．
【答案】OCD；ABO；OD
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：795引用：6難度：0.7
相似題
-
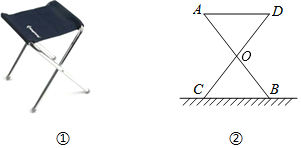1．某大學計劃為新生配備如圖①所示的折疊凳．圖②是折疊凳撐開后的側面示意圖（木條等材料寬度忽略不計），其中凳腿AB和CD的長相等，O是它們的中點．為了使折疊凳坐著舒適，廠家將撐開后的折疊凳寬度AD設計為30cm,則由以上信息可推得CB的長度也為30cm,依據是（ ）發布：2024/12/10 13:0:2組卷：622引用：5難度：0.5 -
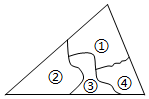2．打碎的一塊三角形玻璃如圖所示，現在要去玻璃店配一塊完全一樣的玻璃，最省事的方法是（ ）發布：2024/12/15 21:30:2組卷：4329引用：31難度：0.5 -
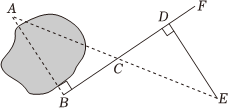3．如圖，要測量池塘兩岸相對的兩點A，B的距離，小明在池塘外取AB的垂線BF上的點C，D，使BC=CD，再畫出BF的垂線DE，使E與A，C在一條直線上，這時測得DE的長就是AB的長，依據是（ ）發布：2024/12/18 6:0:2組卷：4234引用：38難度：0.5