【問題提出】:
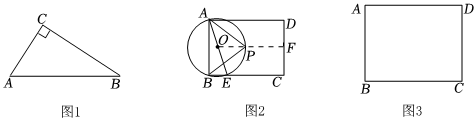
(1)如圖1,在Rt△ACB中,∠ACB=90°,AC=5,BC=12,則cos∠BAC=513513.
【問題探究】:
(2)如圖2,在矩形ABCD中,AB=6,BC=8,在矩形內部有一動點P,滿足tan∠APB=3.小明打算找出P到CD的最短距離.他的操作如下:
在BC上取一點E,使得BE=2,連接AE,作△ABE的外接圓,圓心為O,AE為直徑,過點O作CD的垂線,交⊙O于點P,交CD于點F,此時P到CD的距離最短.
問:以上操作是否合理?若合理,請求出P到CD的最短距離.若不合理,請說明理由.
【問題解決】:
(3)如圖3,某學校的人工智能教室是矩形ABCD形狀,其中AB=8米,BC=10米,為了提高課堂上小組合作學習的效率,學校想把教室設計成幾部分.設計思路如下:在矩形ABCD內部找一點P,連接AP,BP,DP,使得S△APD=59S四邊形ABPD,且cos∠APB=35.其中△APD是老師課堂展示部分,△ABP是小組合作交流部分,剩下的四邊形BCDP是學生創造性設計部分.請計算課堂展示部分△APD的面積.
5
13
5
13
S
△
APD
=
5
9
S
四邊形
ABPD
cos
∠
APB
=
3
5
【考點】圓的綜合題.
【答案】
5
13
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/9/24 0:0:9組卷:294引用:1難度:0.2
相似題
-
1.如圖1,菱形ABCD的邊長為12cm,∠B=60°,M,N分別在邊AB,CD.上,AM=3cm,DN=4cm,點P從點M出發,沿折線MB-BC以1cm/s的速度向點C勻速運動(不與點C重合);△APC的外接圓⊙O與CD相交于點E,連接PE交AC于點F.設點P的運動時間為t s.
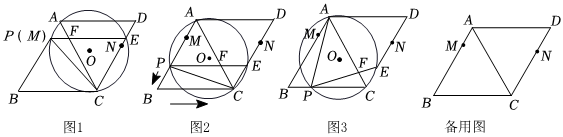
(1)∠APE=°;
(2)若⊙O與AD相切,
①判斷⊙O與CD的位置關系;
②求的長;?APC
(3)如圖3,當點P在BC上運動時,求CF的最大值,并判斷此時PE與AC的位置關系;
(4)若點N在⊙O的內部,直接寫出t的取值范圍.發布:2025/5/24 9:0:1組卷:178引用:3難度:0.1 -
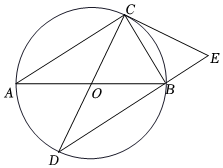 2.如圖,△ABC內接于⊙O,AB,CD是⊙O的直徑,E是DB延長線上一點,且∠DEC=∠ABC.
2.如圖,△ABC內接于⊙O,AB,CD是⊙O的直徑,E是DB延長線上一點,且∠DEC=∠ABC.
(1)求證:CE是⊙O的切線;
(2)若DE=4,AC=2BC,求線段CE的長.5發布:2025/5/24 9:0:1組卷:1754引用:15難度:0.3 -
3.如圖,AB是⊙O的直徑,點D是
上的一點,且∠BDE=∠CBE,BD與AE交于F點.?AE
(1)求證BC是圓O的切線;
(2)若BD平分∠ABE,求證:DE2=DF?DB;
(3)在(2)的條件下,延長ED、BA交于點P,若PA=AO,DE=2,求⊙O的半徑.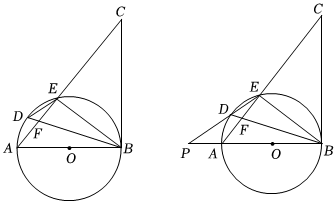 發布:2025/5/24 9:0:1組卷:178引用:2難度:0.3
發布:2025/5/24 9:0:1組卷:178引用:2難度:0.3


