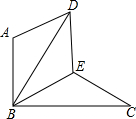
如圖，△BAD是由△BEC在平面內繞點B逆時針旋轉60°而得，且AB⊥BC，BE=CE，連接DE．
（1）求證：△BDE≌△BCE；
（2）試判斷四邊形ABED的形狀．并說明理由．
【考點】全等三角形的判定與性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/13 16:0:1組卷：814引用：21難度：0.3
相似題
-
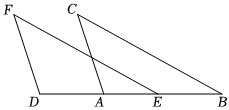1．如圖，EF=BC，DF=AC，DA=EB．求證：∠F=∠C．發布：2025/6/14 11:30:1組卷：3061引用：25難度：0.7 -
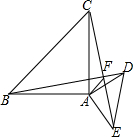2．如圖，AB=AC，AD=AE，∠BAC=∠DAE=90°．
（1）求證：△ABD≌△ACE；
（2）求證：CE⊥BD；
（3）求∠AFB的度數．發布：2025/6/14 11:30:1組卷：314引用：1難度：0.9 -
3．仔細閱讀下面的解題過程，并完成填空：
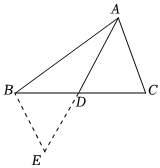
如圖，AD為△ABC的中線，已知AD=4cm,試確定AB+AC的取值范圍．
解：延長AD到E，使DE=AD，連接BE．
因為AD為△ABC的中線，
所以 ，
在△ACD和△EBD中，因為AD=DE，∠ADC=∠EDB，CD=BD，所以 （SAS）．
所以BE=AC（ ）．
因為AB+BE＞AE（ ），
所以AB+AC＞AE．
因為AE=2AD=8cm,所以AB+AC＞cm.發布：2025/6/14 12:0:1組卷：96引用：1難度：0.7