已知圓O：x2+y2=4，點(diǎn)P為直線l：x=4上的動(dòng)點(diǎn)．
（Ⅰ）若從P到圓O的切線長為23，求P點(diǎn)的坐標(biāo)以及兩條切線所夾劣弧長；
（Ⅱ）若點(diǎn)A（-2，0），B（2，0），直線PA，PB與圓O的另一個(gè)交點(diǎn)分別為M，N，求證：直線MN經(jīng)過定點(diǎn)（1，0）．
2
3
【考點(diǎn)】直線和圓的方程的應(yīng)用．
【答案】（I）（4，0），．
（II）設(shè)M（x1，y1），N（x2，y2），Q（1，0），
依題意，直線PA經(jīng)過點(diǎn)A（-2，0），P（4，t），
可以設(shè)，
和圓x2+y2=4聯(lián)立，得到
，
代入消元得到，（t2+36）x2+4t2x+4t2-144=0，
因?yàn)橹本€AP經(jīng)過點(diǎn)A（-2，0），M（x1，y1），所以-2，x1是方程的兩個(gè)根，
所以有，，
代入直線方程得，．
同理，設(shè)，聯(lián)立方程有
，
代入消元得到（4+t2）x2-4t2x+4t2-16=0，
因?yàn)橹本€BP經(jīng)過點(diǎn)B（2，0），N（x2，y2），所以2，x2是方程的兩個(gè)根，，，
代入得到．
若x1=1，則t2=12，此時(shí)
顯然M，Q，N三點(diǎn)在直線x=1上，即直線MN經(jīng)過定點(diǎn)Q（1，0），
若x1≠1，則t2≠12，x2≠1，
所以有，，
所以kMQ=kNQ，所以M，N，Q三點(diǎn)共線，
即直線MN經(jīng)過定點(diǎn)Q（1，0）．
綜上所述，直線MN經(jīng)過定點(diǎn)Q（1，0）．
4
π
3
（II）設(shè)M（x1，y1），N（x2，y2），Q（1，0），
依題意，直線PA經(jīng)過點(diǎn)A（-2，0），P（4，t），
可以設(shè)
AP
：
y
=
t
6
（
x
+
2
）
和圓x2+y2=4聯(lián)立，得到
y = t 6 （ x + 2 ） |
x 2 + y 2 = 4 |
代入消元得到，（t2+36）x2+4t2x+4t2-144=0，
因?yàn)橹本€AP經(jīng)過點(diǎn)A（-2，0），M（x1，y1），所以-2，x1是方程的兩個(gè)根，
所以有
-
2
x
1
=
4
t
2
-
144
t
2
+
36
x
1
=
72
-
2
t
2
t
2
+
36
代入直線方程
y
=
t
6
（
x
+
2
）
y
1
=
t
6
（
72
-
2
t
2
t
2
+
36
+
2
）
=
24
t
t
2
+
36
同理，設(shè)
BP
：
y
=
t
2
（
x
-
2
）
y = t 2 （ x - 2 ） |
x 2 + y 2 = 4 |
代入消元得到（4+t2）x2-4t2x+4t2-16=0，
因?yàn)橹本€BP經(jīng)過點(diǎn)B（2，0），N（x2，y2），所以2，x2是方程的兩個(gè)根，
2
x
2
=
4
t
2
-
16
t
2
+
4
x
2
=
2
t
2
-
8
t
2
+
4
代入
y
=
t
2
（
x
-
2
）
y
2
=
t
2
（
2
t
2
-
8
t
2
+
4
-
2
）
=
-
8
t
t
2
+
4
若x1=1，則t2=12，此時(shí)
x
2
=
2
t
2
-
8
t
2
+
4
=
1
顯然M，Q，N三點(diǎn)在直線x=1上，即直線MN經(jīng)過定點(diǎn)Q（1，0），
若x1≠1，則t2≠12，x2≠1，
所以有
k
MQ
=
y
1
-
0
x
1
-
1
=
24
t
t
2
+
36
72
-
2
t
2
t
2
+
36
-
1
=
8
t
12
-
t
2
k
NQ
=
y
2
-
0
x
2
-
1
=
-
8
t
t
2
+
4
2
t
2
-
8
t
2
+
4
-
1
=
-
8
t
t
2
-
12
所以kMQ=kNQ，所以M，N，Q三點(diǎn)共線，
即直線MN經(jīng)過定點(diǎn)Q（1，0）．
綜上所述，直線MN經(jīng)過定點(diǎn)Q（1，0）．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：333引用：18難度：0.1
相似題
-
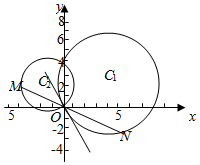1．已知圓C1：（x-4）2+（y-2）2=20與y軸交于O，A兩點(diǎn)，圓C2過O，A兩點(diǎn)，且直線C2O與圓C1相切；
（1）求圓C2的方程；
（2）若圓C2上一動(dòng)點(diǎn)M，直線MO與圓C1的另一交點(diǎn)為N，在平面內(nèi)是否存在定點(diǎn)P使得PM=PN始終成立，若存在求出定點(diǎn)坐標(biāo)，若不存在，說明理由．發(fā)布：2024/10/16 15:0:1組卷：547引用：7難度：0.3 -
2．若直線ax+y=0始終平分圓x2+y2-2ax+2ay+2a2+a-1=0的周長，則a的值為（ ）
發(fā)布：2024/12/8 10:30:3組卷：357引用：2難度：0.8 -
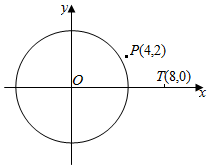3．已知直角坐標(biāo)系xOy中，圓O：x2+y2=16．
①過點(diǎn)P（4，2）作圓O的切線m,求m的方程；
②直線l：y=kx+b與圓O交于點(diǎn)M，N兩點(diǎn)，已知T（8，0），若x軸平分∠MTN，證明：不論k取何值，直線l與x軸的交點(diǎn)為定點(diǎn)，并求出此定點(diǎn)坐標(biāo)．發(fā)布：2024/9/25 3:0:1組卷：147引用：2難度：0.6