如圖，點P是正方形ABCD對角線AC上一動點，點E在射線BC上，且PE=PB，連接PD，O為AC中點．
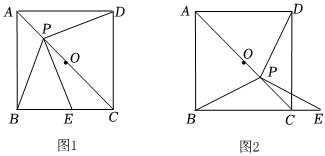
（1）如圖1，當點P在線段OA上時，試猜想PE與PD的數量關系和位置關系．
（2）如圖2，當點P在線段OC上時，（1）中的猜想還成立嗎？請說明理由．
（3）如圖2，試用等式來表示PB、BC、CE之間的數量關系：BC2+CE2=2PB2BC2+CE2=2PB2．
【考點】四邊形綜合題．
【答案】BC2+CE2=2PB2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/8 18:0:1組卷：53引用：1難度：0.1
相似題
-
1．（1）如圖1，在四邊形ABCD中，DA=DC，∠A=∠C=90°，E、F分別是邊AB、BC上的點，且∠EDF=
∠ADC，請直接寫出圖中線段AE、EF、FC之間的數量關系 ．12
（2）如圖2，在四邊形ABCD中，DA=DC，∠A+∠C=180°，E、F分別是邊AB、BC上的點，且∠EDF=∠ADC，上述結論是否仍然成立，并說明理由．12
（3）如圖3，在四邊形ABCD中，DA=DC，∠A+∠BCD=180°，E、F分別是邊AB、BC延長線上的點，且∠EDF=∠ADC，（1）中的結論是否仍然成立？若成立，請證明；若不成立，線段AE、EF、FC之間又有怎樣的數量關系，請直接寫出你的猜想，并說明理由．12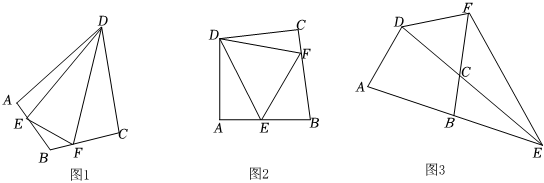
發布：2025/6/9 2:30:1組卷：165引用：1難度：0.2 -
2．矩形ABCD中，∠ACB=30°，△BEF中，∠BEF=90°，∠BFE=30°，BF=
AC，連接FD，點G是FD中點，將△BEF繞點B順時針旋轉α（0°＜α＜360°）．12
（1）如圖1，若點B恰好在線段DF延長線上，AB=4，連接EG，求EG的長度；
（2）如圖2，若點E恰好落在線段FD上，連接AG，證明：2（GD-GA）=DC；3
（3）如圖3，若點E恰好落在線段AB延長線上，點M是線段AD上一點，3AM=DM，N是平面內一點，滿足∠MND=∠FDC，已知AB=4，當△DMN是等腰三角形時，直接寫出線段MN的長度．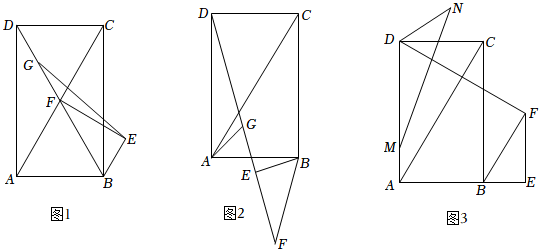
發布：2025/6/9 1:0:1組卷：118引用：1難度：0.1 -
3．問題情境：數學活動課上，老師組織同學們以“正方形”為主題開展數學活動．
動手實踐：
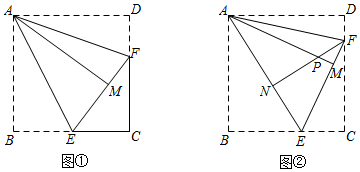
（1）如圖①，已知正方形紙片ABCD，勤奮小組將正方形紙片沿過點A的直線折疊，使點B落在正方形ABCD的內部，點B的對應點為點M，折痕為AE，再將紙片沿過點A的直線折疊，使AD與AM重合，折痕為AF，易知點E、M、F共線，則∠EAF=度．
拓展應用：
（2）如圖②，騰飛小組在圖①的基礎上進行如下操作：將正方形紙片沿EF繼續折疊，使得點C的對應點為點N，他們發現，當點E的位置不同時，點N的位置也不同，當點E在BC邊的某一位置時，點N恰好落在折痕AE上．
①則∠CFE=度．
②設AM與NF的交點為點P，運用（1）、（2）操作所得結論，求證：△ANP≌△FNE．
解決問題：
（3）在圖②中，若AB=3，請直接寫出線段MP的長．發布：2025/6/9 2:0:7組卷：1098引用：9難度：0.3