對于任意一個四位自然數(shù)m,若滿足百位上的數(shù)字與十位上的數(shù)字之和等于千位上的數(shù)字與個位上的數(shù)字之差的兩倍，則稱這個數(shù)為“富貴數(shù)”．將“富貴數(shù)”m的千位上的數(shù)字與個位上的數(shù)字交換位置，百位上的數(shù)字與十位上的數(shù)字交換位置，得到新數(shù)m'，記F（m）=m+m'．如：7514滿足5+1=2×（7-4），則7514是一個“富貴數(shù)”，F(xiàn)（7514）=7514+4157=11671．
（1）判斷7353和6591是不是“富貴數(shù)”；
（2）證明：對任意一個“富貴數(shù)”m,其F（m）都能被11整除；
（3）已知某“富貴數(shù)”s,滿足條件s=8000+100a+10b+c（1≤a≤9，1≤b≤7，1≤c≤8且均為整數(shù)）．記G（s）=F（s）11，若G（s）能被7整除，求出所有滿足條件的s的值．
G
（
s
）
=
F
（
s
）
11
【考點】整數(shù)問題的綜合運用．
【答案】（1）7353是“富貴數(shù)”，6591不是“富貴數(shù)”；
（2）證明見解析；
（3）8951，8661，8771．
（2）證明見解析；
（3）8951，8661，8771．
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：203引用：2難度：0.2
相似題
-
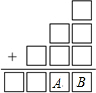1．在右邊的加法算式中，每一個□表示一個數(shù)字，任意兩個數(shù)字都不相同，那么A與B乘積的最大值是．發(fā)布：2025/5/28 16:0:1組卷：41引用：1難度：0.5 -
2．x,y為正整數(shù)，且兩個分數(shù)之和
也是整數(shù)，求證：這兩個分數(shù)都是整數(shù)．x2-1y+1+y2-1x+1發(fā)布：2025/5/28 16:0:1組卷：66引用：1難度：0.1 -
3．已知下面等式對任意實數(shù)x都成立（n為正整數(shù)）：（1+x）+（1+x）2+（1+x）3+…+（1+x）n=a0+a1x+a2x2+…+anxn，且a1+a2+a3+…+an=57，則滿足條件的n的可能值是
．發(fā)布：2025/5/28 16:30:2組卷：78引用：2難度：0.5