給定函數f（x）=x+1，g（x）=x2+2x+1．
（1）在同一直角坐標系中畫出函數f（x），g（x）的圖像；
（2）?x∈R，用M（x）表示f（x），g（x）中的最小者，記為M（x）=min{f（x），g（x）}例如，當x=2時，M（2）=min{f（2），g（2）}=M{3，9}=3請用解析法表示函數M（x）．
【考點】解析法表示函數．
【答案】（1）詳見解答過程；
（2）M（x）=
．
（2）M（x）=
x 2 + 2 x + 1 ，- 1 ＜ x ＜ 0 |
x + 1 ， x ≥ 0 或 x ≤ - 1 |
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：18引用：1難度：0.7
相似題
-
1．給定函數f（x）=x+3，g（x）=（x+1）2，x∈R．
（1）在同一坐標系中畫出函數f（x），g（x）的圖像，
（2）若min{a,b}表示a,b中的較小者，例如min{2，1}=1．記m（x）=min{f（x），g（x）}．
（i）請分別用圖像法和解析法表示函數m（x），并指出函數m（x）的單調區間，
（ii）當時，求m（x）的最大值和最小值．x∈[-52，-12]發布：2024/8/9 8:0:9組卷：143引用：5難度：0.8 -
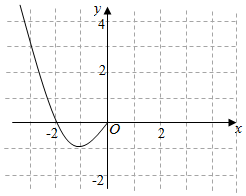2．已知函數f（x）是定義在R上的偶函數，且當x≤0時，f（x）=x2+2x.現已畫出函數f（x）在y軸左側的圖象，如圖所示，并根據圖象完成下列問題：
（1）補全f（x）的圖像，寫出函數f（x），x∈R的增區間；
（2）求f（-4）和f（3）的值；
（3）求出函數f（x），x∈R的解析式．發布：2024/6/27 10:35:59組卷：38引用：1難度：0.8 -
3．已知函數f（x）=|x-2|+x2．
（1）去掉絕對值，寫出f（x）的分段解析式；
（2）畫出f（x）的圖象，并寫出f（x）的最小值．發布：2024/6/27 10:35:59組卷：109引用：2難度：0.8