數學來源于生活，生活中處處有數學，用我們平時喝的糖水做“糖水實驗”也能驗證發現一些數學結論．現有a克糖水，其中含有b克糖（a＞b＞0），則糖水的濃度（即糖的質量與糖水的質量比）為ba．
（1）糖水實驗一：加入m克水，則糖水的濃度為 ba+mba+m．生活經驗告訴我們，糖水加水后會變淡，由此可以寫出一個不等式 ba+m＜baba+m＜ba，我們趣稱為“糖水不等式”．
（2）糖水實驗二：
將“糖水實驗一”中的“加入m克水”改為“加入m克糖”，則糖水的濃度為 b+ma+mb+ma+m．根據生活經驗，請你寫出一個新的“糖水不等式”b+ma+m＞bab+ma+m＞ba．
（3）請結合（2）探究得到的結論嘗試證明：
設a、b、c為△ABC三邊的長，求證：ca+b+ab+c+ba+c＜2．#ZZ011
b
a
b
a
+
m
b
a
+
m
b
a
+
m
＜
b
a
b
a
+
m
＜
b
a
b
+
m
a
+
m
b
+
m
a
+
m
b
+
m
a
+
m
＞
b
a
b
+
m
a
+
m
＞
b
a
c
a
+
b
+
a
b
+
c
+
b
a
+
c
＜
2
【考點】三角形綜合題．
【答案】；；；
b
a
+
m
b
a
+
m
＜
b
a
b
+
m
a
+
m
b
+
m
a
+
m
＞
b
a
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/4 8:0:9組卷：286引用：4難度：0.5
相似題
-
1．已知在△ABC中，AC=BC，∠BAC=60°，點P在△ABC外，連接BP、CP，且AB=BP．
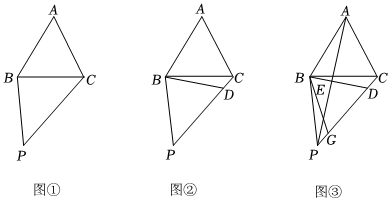
（1）如圖①，求證：BP=BC；
（2）如圖②，作∠ABP的平分線交CP于點D，求∠BDC的度數；
（3）如圖③，在（2）的條件下，連接AP交BD于點E，在CP上取一點G，連接BG，若BG=8，BE=3，CD=2，求證：△BCD≌△BPG．發布：2025/5/31 14:30:1組卷：236引用：2難度：0.1 -
2．（1）問題發現：如圖1，已知：在△ABC中，∠BAC=90°，AB=AC，直線m經過點A，BD⊥直線m,CE⊥直線m,垂足分別為點D、E．試寫出線段DE，BD和CE之間的數量關系為；
（2）思考探究：如圖2，將（1）中的條件改為：在△ABC中，AB=AC，D，A、E三點都在直線m上，并且∠BDA=∠AEC=∠BAC=α，其中α為任意銳角或鈍角．請問（1）中結論還是否成立？若成立，請給出證明；若不成立，請說明理由．
（3）拓展應用：如圖3，D、E是D、A、E三點所在直線m上的兩動點（D，A，E三點互不重合），點F為∠BAC平分線上的一點，且△ABF和△ACF均為等邊三角形，連接BD，CE，若∠BDA=∠AEC=∠BAC，試判斷△DEF的形狀并說明理由．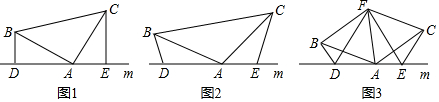
發布：2025/5/31 17:30:1組卷：538引用：11難度：0.3 -
3．（1）閱讀理解：如圖1，在△ABC中，若AB=3，AC=5．求BC邊上的中線AD的取值范圍，小聰同學是這樣思考的：延長AD至E，使DE=AD，連接BE．利用全等將邊AC轉化到BE，在△BAE中利用三角形三邊關系即可求出中線AD的取值范圍，在這個過程中小聰同學證三角形全等用到的判定方法是 ，中線AD的取值范圍是 ；
（2）問題解決：如圖2，在△ABC中，點D是BC的中點，DM⊥DN．DM交AB于點M，DN交AC于點N．求證：BM+CN＞MN；
（3）問題拓展：如圖3，在△ABC中，點D是BC的中點，分別以AB，AC為直角邊向△ABC外作Rt△ABM和Rt△ACN，其中∠BAM=∠NAC=90°，AB=AM，AC=AN，連接MN，請你探索AD與MN的數量與位置關系，并直接寫出AD與MN的關系．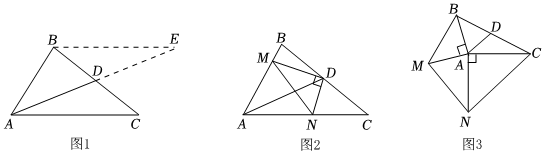
發布：2025/5/31 17:30:1組卷：357引用：20難度：0.1