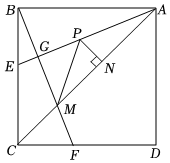
如圖，正方形ABCD的邊長為6，點E，F分別為邊BC，CD上兩點，CF=BE，AE平分∠BAC，連接BF，分別交AE，AC于點G，M，點P是線段AG上的一個動點，過點P作PN⊥AC，垂足為N，連接PM，下列說法正確的是 ①③④①③④．（填序號）
①△ABE≌△BCF；②AM=42； ③S△AGM=922； ④PM+PN的最小值為32
2
9
2
2
2
【答案】①③④
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 7:30:1組卷：449引用：1難度：0.6
相似題
-
1．如圖，正方形ABCD的邊長為4，E是BC的中點，點P是AC邊上的一個動點，連結BP，EP，則BP+EP的最小值為（ ）發布：2025/5/24 14:30:1組卷：40引用：2難度：0.6 -
2．如圖，在矩形ABCD中，AB=8，AD=4，點E是矩形ABCD內部一動點，且∠BEC=90°，點P是AB邊上一動點，連接PD，PE，則PD+PE的最小值為 ．發布：2025/5/24 11:30:1組卷：426引用：4難度：0.6 -
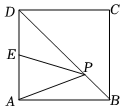3．如圖所示，在邊長為2的正方形ABCD中，E為邊AD的中點，P為對角線BD上的一個動點，連接PA、PE，則PA+PE的最小值是 ．2發布：2025/5/24 14:0:2組卷：129引用：2難度：0.7
相關試卷