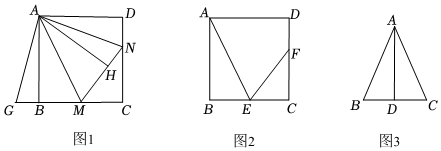
知識再現：已知，如圖1，四邊形ABCD是正方形，點M、N分別在邊BC、CD上，連接AM、AN、MN，且∠MAN=45°，延長CB至G使BG=DN，連接AG，根據三角形全等的知識，我們可以證明MN=BM+DN．
知識探究：（1）如圖1，作AH⊥MN，垂足為點H，猜想AH與AB有什么數量關系？并進行證明．
知識運用：（2）如圖2，四邊形ABCD是正方形，E是邊BC的中點，F為邊CD上一點，且∠FEC=2∠BAE，AB=24，求DF的長．
知識拓展：（3）已知∠BAC=45°，AD⊥BC于點D，且BD=2，AD=6，求CD的長．
【考點】四邊形綜合題．
【答案】（1）AH=AB；證明見解析；
（2）8；
（3）3．
（2）8；
（3）3．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 21:0:1組卷：268引用：2難度：0.4
相似題
-
1．問題背景
（1）如圖，△ABC中，DE∥BC分別交AB，AC于D，E兩點，過點E作EF∥AB交BC于點F．請按圖示數據填空：四邊形DBFE的面積S=，△EFC的面積S1=，△ADE的面積S2=
探究發現
（2）在（1）中，若BF=a,FC=b,DE與BC間的距離為h.請證明S2=4S1S2．
拓展遷移
（3）如圖，?DEFG的四個頂點在△ABC的三邊上，若△ADG、△DBE、△GFC的面積分別為2、5、3，試利用（2）中的結論求△ABC的面積．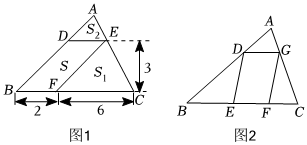
發布：2025/5/25 0:30:1組卷：590引用：6難度：0.5 -
2．定義：若四邊形中某個頂點與其它三個頂點的距離相等，則這個四邊形叫做等距四邊形，這個頂點叫做這個四邊形的等距點．
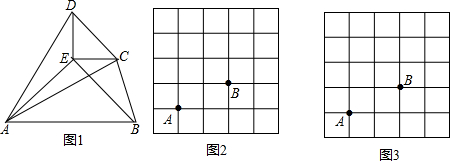
（1）判斷：一個內角為120°的菱形等距四邊形．（填“是”或“不是”）
（2）如圖2，在5×5的網格圖中有A、B兩點，請在答題卷給出的兩個網格圖上各找出C、D兩個格點，使得以A、B、C、D為頂點的四邊形為互不全等的“等距四邊形”，畫出相應的“等距四邊形”，并寫出該等距四邊形的端點均為非等距點的對角線長．
端點均為非等距點的對角線長為端點均為非等距點的對角線長為
（3）如圖1，已知△ABE與△CDE都是等腰直角三角形，∠AEB=∠DEC=90°，連接AD，AC，BC，若四邊形ABCD是以A為等距點的等距四邊形，求∠BCD的度數．發布：2025/5/25 0:30:1組卷：636引用：4難度：0.3 -
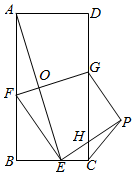3．如圖，在矩形ABCD中，AB=2BC，F、G分別為AB、DC邊上的動點，連接GF，沿GF將四邊形AFGD翻折至四邊形EFGP，點E落在BC上，EP交CD于點H，連接AE交GF于點O．
（1）寫出GF與AE之間的位置關系是：；
（2）求證：AE=2GF；
（3）連接CP，若sin∠CGP=，GF=35，求CE的長．10發布：2025/5/25 0:30:1組卷：2006引用：7難度：0.2