【概念學習】
在平面直角坐標系xOy中，⊙O的半徑為1，若⊙O平移d個單位后，使某圖形上所有點在⊙O內或⊙O上，則稱d的最小值為⊙O對該圖形的“最近覆蓋距離”．例如，如圖①，A（3，0），B（4，0），則⊙O對線段AB的“最近覆蓋距離”為3．
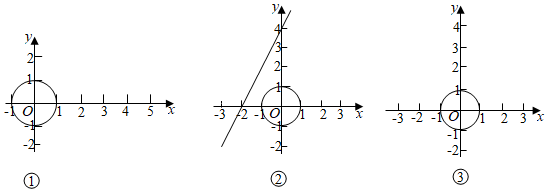
【概念理解】
（1）⊙O對點（3，4）的“最近覆蓋距離”為 44．
（2）如圖②，點P是函數y=2x+4圖象上一點，且⊙O對點P的“最近覆蓋距離”為3，則點P的坐標為 （0，4）或（-165，-125）（0，4）或（-165，-125）．
【拓展應用】
（3）如圖③，若一次函數y=kx+4的圖象上存在點C，使⊙O對點C的“最近覆蓋距離”為1，求k的取值范圍．
（4）D（3，m）、E（4，m+1），且-4＜m＜2，將⊙O對線段DE的“最近覆蓋距離”記為d,則d的取值范圍是 3≤d＜323≤d＜32．
16
5
12
5
16
5
12
5
2
2
【考點】圓的綜合題．
【答案】4；（0，4）或（-，-）；3≤d＜3
16
5
12
5
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 4:0:7組卷：1245引用：3難度：0.3
相似題
-
1．已知⊙O的直徑AB=2，弦AC與弦BD交于點E，且OD⊥AC，垂足為點F．
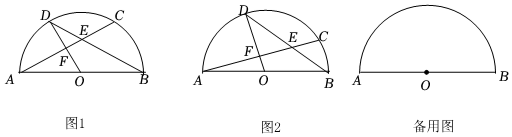
（1）如圖1，若AC=BD，求線段DE的長．
（2）如圖2，若DE：BE=3：2，求∠ABD的正切值．
（3）連結BC，CD，DA，若BC是⊙O的內接正n邊形的一邊，CD是⊙O的內接正2n邊形的一邊，求△ACD的面積．發布：2025/5/24 21:30:1組卷：239引用：1難度：0.3 -
2．在Rt△ABC中，∠C=90°．
（1）如圖①，點O在斜邊AB上，以點O為圓心，OB長為半徑的圓交AB于點D，交BC于點E，與邊AC相切于點F．求證：∠1=∠2；
（2）在圖②中作⊙M，使它滿足以下條件：
①圓心在邊AB上；②經過點B；③與邊AC相切．
（尺規作圖，只保留作圖痕跡，不要求寫出作法）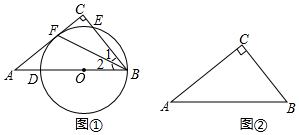
發布：2025/5/24 21:30:1組卷：833引用：9難度：0.3 -
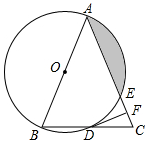3．如圖，在△ABC中，AB=AC，以AB為直徑的⊙O分別與BC，AC交于點D，E，過點D作DF⊥AC，垂足為點F．
（1）求證：直線DF是⊙O的切線；
（2）求證：BC2=4CF?AC；
（3）若⊙O的半徑為4，∠CDF=15°，求陰影部分的面積．發布：2025/5/24 21:0:1組卷：2988引用：17難度：0.5