2023年江蘇省揚州中學教育集團樹人學校中考數學一模試卷

一、選擇題（共8小題）

• 1．-7的倒數是（　　）

  A．7

  B． 1 7

  C．-7

  D．- 1 7
  組卷：780引用：204難度：0.9

  解析

• 2．下列計算正確的是（　　）

  A．2m+3n=5mn

  B．m2?m3=m6

  C．m8÷m6=m2

  D．（-m）3=m3
  組卷：73引用：7難度：0.9

  解析

• 3．若x+y=2，z-y=-3，則x+z的值等于（　　）

  A．5

  B．1

  C．-1

  D．-5
  組卷：3434引用：31難度：0.7

  解析

• 4．某小組7名學生的中考體育分數如下：37，40，39，37，40，38，40，該組數據的眾數、中位數分別為（　　）

  A．40，37

  B．40，39

  C．39，40

  D．40，38
  組卷：690引用：7難度：0.8

  解析

• 5．已知x₁，x₂是一元二次方程x²+x-3=0的兩個根，則x₁+x₂-x₁x₂的值為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：719引用：7難度：0.8

  解析

• 6．已知二次函數y=ax²+bx+c中，函數y與自變量x的部分對應值如表，以下結論正確的是（　　）

  x	…	-1	0	1	2	3	…
  y	…	3	0	-1	m	3	…

  A．拋物線y=ax2+bx+c的開口向下

  B．當x＜3時，y隨x增大而增大

  C．當y＞0時，x的取值范圍是0＜x＜2

  D．方程ax2+bx+c=0的根為0和2
  組卷：1408引用：5難度：0.5

  解析

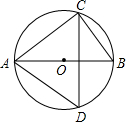• 7．如圖，AB是⊙O的直徑，點C、D在⊙O上，若∠CAB=40°，則∠ADC的度數為（　　）

  A．25°

  B．30°

  C．45°

  D．50°
  組卷：613引用：7難度：0.9

  解析

• 8．如圖1，在菱形ABCD中，∠A=60°，動點P從點A出發，沿折線AD→DC→CB方向勻速運動，運動到點B停止．設點P的運動路程為x,△APB的面積為y,y與x的函數圖象如圖2所示，則AB的長為（　　）
  

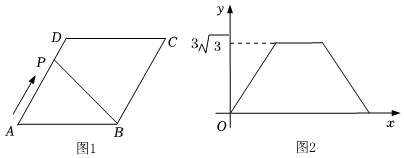
  A． 3

  B．2 3

  C．3 3

  D．4 3
  組卷：2437引用：29難度：0.6

  解析

二、填空題（共10小題）

• 9．若式子

  x

  -

  2

  在實數范圍內有意義，則x的取值范圍是

  ．
  組卷：2046引用：76難度：0.7

  解析

三、解答題

• 27．綜合與實踐
  問題情境：在Rt△ABC中，∠BAC=90°，AB=6，AC=8．直角三角板EDF中∠EDF=90°，將三角板的直角頂點D放在Rt△ABC斜邊BC的中點處，并將三角板繞點D旋轉，三角板的兩邊DE，DF分別與邊AB，AC交于點M，N．
  猜想證明：
  （1）如圖①，在三角板旋轉過程中，當點M為邊AB的中點時，試判斷四邊形AMDN的形狀，并說明理由；
  問題解決：
  （2）如圖②，在三角板旋轉過程中，當∠B=∠MDB時，求線段CN的長；
  （3）如圖③，在三角板旋轉過程中，當AM=AN時，直接寫出線段AN的長．
  
  組卷：1355引用：22難度：0.3

  解析

• 28．【概念學習】
  在平面直角坐標系xOy中，⊙O的半徑為1，若⊙O平移d個單位后，使某圖形上所有點在⊙O內或⊙O上，則稱d的最小值為⊙O對該圖形的“最近覆蓋距離”．例如，如圖①，A（3，0），B（4，0），則⊙O對線段AB的“最近覆蓋距離”為3．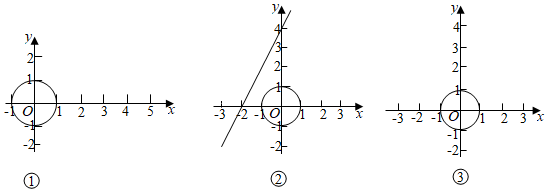
  
  【概念理解】
  （1）⊙O對點（3，4）的“最近覆蓋距離”為

  ．
  （2）如圖②，點P是函數y=2x+4圖象上一點，且⊙O對點P的“最近覆蓋距離”為3，則點P的坐標為

  ．
  【拓展應用】
  （3）如圖③，若一次函數y=kx+4的圖象上存在點C，使⊙O對點C的“最近覆蓋距離”為1，求k的取值范圍．
  （4）D（3，m）、E（4，m+1），且-4＜m＜2，將⊙O對線段DE的“最近覆蓋距離”記為d,則d的取值范圍是

  ．
  組卷：1245引用：3難度：0.3

  解析