當(dāng)前位置：
2022-2023學(xué)年重慶市長(zhǎng)壽區(qū)川維中學(xué)九年級(jí)（下）第一次定時(shí)訓(xùn)練數(shù)學(xué)試卷>
試題詳情
正方形ABCD，點(diǎn)E為平面內(nèi)一點(diǎn)，連接BE，將BE繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°得到BF，連接AF，CE．已知點(diǎn)M為CE的中點(diǎn)，連接BM．
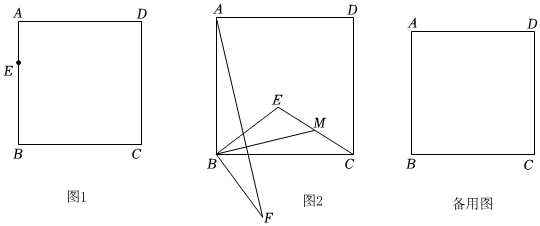
（1）如圖1．
①若點(diǎn)E為邊AB邊上一點(diǎn)，補(bǔ)全圖形；
②判斷并證明線段BM和AF的數(shù)量關(guān)系．
（2）如圖2，若點(diǎn)E是ABCD的內(nèi)部一點(diǎn)，（1）中線段BM和AF的數(shù)量關(guān)系是否仍然成立，如果成立，請(qǐng)證明；如果不成立，請(qǐng)說(shuō)明理由．
【考點(diǎn)】四邊形綜合題．
【答案】（1）①見(jiàn)解析，②，見(jiàn)解析；
（2）成立，見(jiàn)解析．
BM
=
1
2
AF
（2）成立，見(jiàn)解析．
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：114引用：3難度：0.3
相似題
-
1．已知：菱形ABCD和菱形A′B′C′D′，∠BAD=∠B′A′D′，起始位置點(diǎn)A在邊A′B′上，點(diǎn)B在A′B′所在直線上，點(diǎn)B在點(diǎn)A的右側(cè)，點(diǎn)B′在點(diǎn)A′的右側(cè)，連接AC和A′C′，將菱形ABCD以A為旋轉(zhuǎn)中心逆時(shí)針旋轉(zhuǎn)α角（0°＜α＜180°）．
（1）如圖1，若點(diǎn)A與A′重合，且∠BAD=∠B′A′D′=90°，求證：BB′=DD′．
（2）若點(diǎn)A與A′不重合，M是A′C′上一點(diǎn)，當(dāng)MA′=MA時(shí)，連接BM和A′C，BM和A′C所在直線相交于點(diǎn)P．
①如圖2，當(dāng)∠BAD=∠B′A′D′=90°時(shí)，請(qǐng)猜想線段BM和線段A′C的數(shù)量關(guān)系及∠BPC的度數(shù)．
②如圖3，當(dāng)∠BAD=∠B′A′D′=60°時(shí)，請(qǐng)求出線段BM和線段A′C的數(shù)量關(guān)系及∠BPC的度數(shù)．
③在②的條件下，若點(diǎn)A與A′B′的中點(diǎn)重合，A′B′=4，AB=2，在整個(gè)旋轉(zhuǎn)過(guò)程中，當(dāng)點(diǎn)P與點(diǎn)M重合時(shí)，請(qǐng)直接寫(xiě)出線段BM的長(zhǎng)．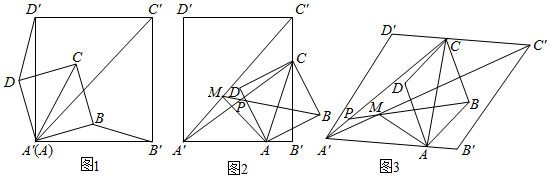
發(fā)布：2025/5/23 3:30:1組卷：1720引用：3難度：0.1 -
2．如圖，在平面直角坐標(biāo)系中，矩形ABCD的邊AB在x軸上，AB、BC的長(zhǎng)分別是一元二次方程x2-7x+12=0的兩個(gè)根（BC＞AB），OA=2OB，邊CD交y軸于點(diǎn)E，動(dòng)點(diǎn)P以每秒1個(gè)單位長(zhǎng)度的速度，從點(diǎn)E出發(fā)沿折線段ED-DA向點(diǎn)A運(yùn)動(dòng)，運(yùn)動(dòng)的時(shí)間為t（0≤t＜6）秒，設(shè)△BOP與矩形AOED重疊部分的面積為S．
（1）求點(diǎn)D的坐標(biāo)；
（2）求S關(guān)于t的函數(shù)關(guān)系式，并寫(xiě)出自變量的取值范圍；
（3）在點(diǎn)P的運(yùn)動(dòng)過(guò)程中，是否存在點(diǎn)P，使△BEP為等腰三角形？若存在，直接寫(xiě)出點(diǎn)P的坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．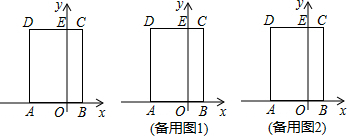
發(fā)布：2025/5/23 3:30:1組卷：862引用：5難度：0.4 -
3．【推理】
如圖1，在邊長(zhǎng)為10的正方形ABCD中，點(diǎn)E是CD上一動(dòng)點(diǎn)，將正方形沿著B(niǎo)E折疊，點(diǎn)C落在點(diǎn)F處，連結(jié)BE，CF，延長(zhǎng)CF交AD于點(diǎn)G，BE與CG交于點(diǎn)M．
（1）求證：CE=DG．
【運(yùn)用】
（2）如圖2，在【推理】條件下，延長(zhǎng)BF交AD于點(diǎn)H．若CE=6，求線段DH的長(zhǎng)．
【拓展】
（3）如圖3，在【推理】條件下，連結(jié)AM．則線段AM的最小值為 ．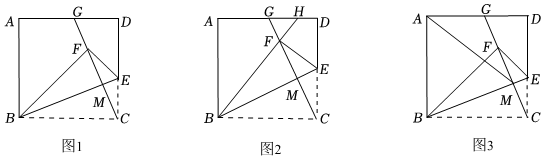
發(fā)布：2025/5/23 4:0:1組卷：423引用：5難度：0.4