閱讀并解答下列問題；在學習完《中心對稱圖形》一章后，老師給出了以下一個思考題：如圖1，在平面直角坐標系xOy中，已知點A（0，3），B（5，1），C（a,0），D（a+2，0），連接AC，CD，DB，求AC+CD+DB最小值．
【思考交流】小明：如圖2，先將點A向右平移2個單位長度到點A1，作點B關于x軸的對稱點B1，連接A1B1交x軸于點D，將點D向左平移2個單位長度得到點C，連接AC．BD．此時AC+CD+DB的最小值等于A1B1+CD．
小穎：如圖3，先將點A向右平移2個單位長度到點A1，作點A1關于x軸的對稱點A2，連接A2B可以求解．
小亮：對稱和平移還可以有不同的組合…．
【嘗試解決】在圖2中，AC+CD+DB的最小值是77．
【靈活應用】如圖4，在平面直角坐標系xOy中，已知點A（0，3），B（5，1），C（a,1），D（a+2，0），連接AC，CD，DB，則AC+CD+DB的最小值是32+532+5，此時a=22，并請在圖5中用直尺和圓規作出AC+CD+DB最小時CD的位置（不寫作法，保留作圖痕跡）．
【拓展提升】如圖6，在平面直角坐標系xOy中，已知點A（0，3），C是一次函數y=x圖象上一點，CD與y軸垂直且CD=2（點D在點C右側），連接AC，CD，AD，直接寫出AC+CD+DA的最小值是34+234+2，此時點C的坐標是（98，98）（98，98）．
3
2
+
5
3
2
+
5
34
+
2
34
+
2
9
8
，
9
8
9
8
，
9
8
【考點】一次函數綜合題．
【答案】7；；2；；（）
3
2
+
5
34
+
2
9
8
，
9
8
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1725引用：2難度：0.1
相似題
-
1．如圖，在平面直角坐標系中，點A（1，0），B（0，2），C（-1，-2），直線AB和直線AC的圖象相交于點A，連接BC．
（1）求直線AB和直線AC的函數表達式；
（2）請直接寫出△ABC的面積為 ，在第一象限，直線AC上找一點D，連接BD，當△ABD的面積等于△ABC的面積時，請直接寫出點D的坐標為 ．
（3）點E是直線AB上的一個動點，在坐標軸上找一點F，連接CE，EF，FC，當△CEF是以CE為底邊的等腰直角三角形時，請直接寫出△CEF的面積為 ．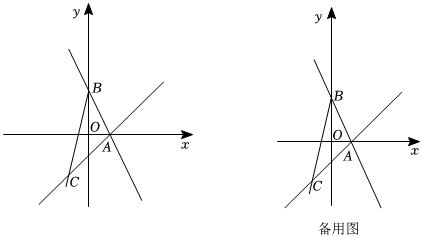
發布：2025/5/29 16:30:1組卷：1030引用：1難度：0.2 -
2．在平面直角坐標系中，一次函數的圖象l1與x軸交于點A，一次函數y=x+6的圖象l2與x軸交于點B，與l1交于點P．直線l3過點A且與x軸垂直，C是l3上的一個動點．y=-43x+43
（1）分別求出點A、P的坐標；
（2）設直線PC對應的函數表達式為y=kx+b,且滿足函數值y隨x的增大而增大．若△PCA的面積為15，分別求出k、b的值；
（3）是否存在點C，使得2∠PCA+∠PAB=90°？若存在，直接寫出點C的坐標；若不存在，請說明理由．發布：2025/5/29 17:30:2組卷：1363引用：3難度：0.4 -
3．如圖，在平面直角坐標系xOy中，直線y=-x+4分別交x軸，y軸于點A，B，點C在x軸的負半軸上，且OC=
OB，點P是線段BC上的動點（點P不與B，C重合），以BP為斜邊在直線BC的右側作等腰Rt△BPD．12
（1）求直線BC的函數表達式；
（2）如圖1，當S△BPD=S△ABC時，求點P的坐標；15
（3）如圖2，連接AP，點E是線段AP的中點，連接DE，OD．試探究∠ODE的大小是否為定值，若是，求出∠ODE的度數；若不是，請說明理由．
發布：2025/5/29 16:0:1組卷：1597引用：2難度：0.1