【問題發現】
（1）如圖1，老師將正方形ABCD和正方形AEFG按如圖所示的位置擺放，連接BE和DG，延長DG交BE的延長線于點H，求BE與DG的數量關系和位置關系；
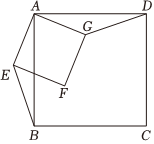
【類比探究】
（2）若將“正方形ABCD和正方形AEFG改成“矩形ABCD和矩形AEFG，且矩形ABCD∽矩形AEFG，AE=3，AG=4，如圖，點E、D、G三點共線，點G在線段DE上時，若AD=12105，求BE的長．
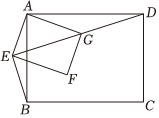
【拓展延伸】
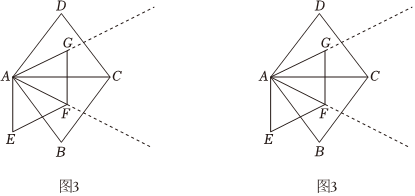
（3）若將“正方形ABCD和正方形AEFG改成“菱形ABCD和菱形AEFG，且菱形ABCD∽菱形AEFG如圖
3，AD=5，AC=6，AG平分∠DAC，點P在射線AG上，在射線AF上截取AQ，使得AQ=35AP，連接PQ，QC，當tan∠PQC=43時，直接寫出AP的長．
AD
=
12
10
5
AQ
=
3
5
AP
tan
∠
PQC
=
4
3
【考點】相似形綜合題．
【答案】（1）BE=DG，BE⊥DG；
（2）3；
（3）AP=或．
（2）3；
（3）AP=
4
5
3
20
5
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/17 8:0:9組卷：698引用：2難度：0.1
相似題
-
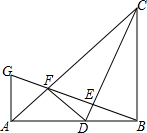1．如圖，在Rt△ABC中，∠ABC=90°．AB=BC．點D是線段AB上的一點，連接CD．過點B作BG⊥CD，分別交CD、CA于點E、F，與過點A且垂直于AB的直線相交于點G，連接DF，給出以下四個結論：①=AGAB；②若點D是AB的中點，則AF=AFFCAB；③當B、C、F、D四點在同一個圓上時，DF=DB；④若23=DBAD，則S△ABC=9S△BDF，其中正確的結論序號是（ ）12發布：2025/6/24 16:30:1組卷：2783引用：11難度：0.2 -
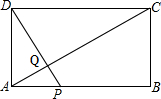2．如圖，矩形ABCD中，AB=20，BC=10，點P為AB邊上一動點，DP交AC于點Q．
（1）求證：△APQ∽△CDQ；
（2）P點從A點出發沿AB邊以每秒1個單位長度的速度向B點移動，移動時間為t秒．
①當t為何值時，DP⊥AC？
②設S△APQ+S△DCQ=y,寫出y與t之間的函數解析式，并探究P點運動到第幾秒到第幾秒之間時，y取得最小值．發布：2025/7/1 13:0:6組卷：2099引用：6難度：0.1 -
3．【探究發現】如圖1，△ABC是等邊三角形，∠AEF=60°，EF交等邊三角形外角平分線CF所在的直線于點F，當點E是BC的中點時，有AE=EF成立；
【數學思考】某數學興趣小組在探究AE、EF的關系時，運用“從特殊到一般”的數學思想，通過驗證得出如下結論：
當點E是直線BC上（B，C除外）任意一點時（其它條件不變），結論AE=EF仍然成立．
假如你是該興趣小組中的一員，請你從“點E是線段BC上的任意一點”；“點E是線段BC延長線上的任意一點”；“點E是線段BC反向延長線上的任意一點”三種情況中，任選一種情況，在備用圖1中畫出圖形，并證明AE=EF．
【拓展應用】當點E在線段BC的延長線上時，若CE=BC，在備用圖2中畫出圖形，并運用上述結論求出S△ABC：S△AEF的值．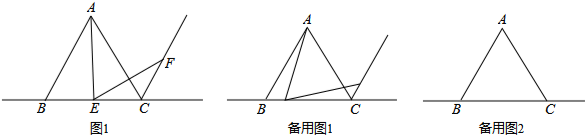
發布：2025/6/24 15:30:2組卷：1873引用：6難度：0.1