求若干個相同的不為零的有理數的除法運算叫做除方．
如：2÷2÷2，（-3）÷（-3）÷（-3）÷（-3）等．類比有理數的乘方，我們把2÷2÷2記作2^③，讀作“2的圈3次方”．（-3）÷（-3）÷（-3）÷（-3）記作（-3）^④，讀作“-3的圈4次方”．
一般地，把

a

÷

a

÷

a

÷?÷

a

n

個

a

（a≠0）記作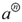，記作“a的圈n次方”．
（1）直接寫出計算結果：2^③=

1

2

1

2

，（-3）^④=

1

9

1

9

．
（2）我們知道，有理數的減法運算可以轉化為加法運算，除法運算可以轉化為乘法運算，請嘗試將有理數的除方運算轉化為乘方運算，歸納如下：一個非零有理數a的圈n次方等于

這個數倒數的（n-2）次方

這個數倒數的（n-2）次方

．
（3）計算24÷2³+（-24）×2^③．