如圖所示的圖形表示勾股定理的一種證明方法，該方法運用了祖沖之的出入相補原理．若圖中空白部分的面積是15，整個圖形（連同空白部分）的面積是39，則大正方形的邊長是（ ）
【考點】勾股定理的證明．
【答案】B
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/30 15:22:31組卷：1095引用：3難度：0.5
相似題
-
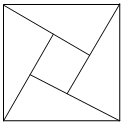1．如圖是在北京召開的國際數學家大會的會標，它是由四個全等的直角三角形與中間一個小正方形拼成的一個大正方形．若小正方形的面積為8，每個直角三角形比小正方形的面積均小1，則每個小直角三角形的周長是（ ）發布：2025/5/31 11:30:1組卷：543引用：5難度：0.5 -
2．我們發現，用不同的方式表示同一圖形的面積可以解決線段長度之間關系的有關問題，這種方法稱為等面積法，這是一種重要的數學方法，請你用等面積法來探究下列兩個問題：
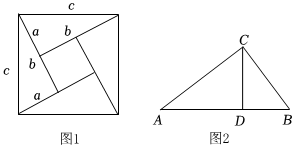
（1）如圖1是著名的“趙爽弦圖”，由四個全等的直角三角形拼成，請你用它驗證勾股定理；
（2）如圖2，在Rt△ABC中∠ACB=90°，CD是AB邊上高，AC=12，BC=5，求CD的長度．發布：2025/6/1 19:0:6組卷：519引用：1難度：0.6 -
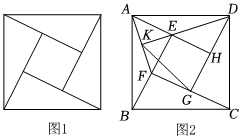3．如圖1，四個全等的直角三角形圍成一個大正方形，中間是個小正方形，這個圖形是我國漢代趙爽在注解《周髀算經》時給出的，人們稱它為“趙爽弦圖”．在弦圖中（如圖2）連結AF，DE，并延長DE交AF于點K，連結KG．若AH=2DH=，則KG的長為（ ）22發布：2025/6/1 1:30:1組卷：531引用：5難度：0.6