古希臘著名的畢達哥拉斯學派把1，3，6，10…這樣的數稱為“三角形數”，而把1，4，9，16…這樣的數稱為“正方形數”．觀察下面的點陣圖和相應的等式，探究其中的規律：
（1）下圖反映了任何一個三角形數是如何得到的，認真觀察，并在④后面的橫線上寫出相應的等式；
①1=1
②1+2=（1+2）×22=3
③1+2+3=（1+3）×32=6
④1+2+3+4=（1+4）×421+2+3+4=（1+4）×42；
（2）通過猜想，寫出（1）中與第九個點陣相對應的等式1+2+3+…+9=（1+9）×921+2+3+…+9=（1+9）×92；
（3）從下圖中可以發現，任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和．結合（1）觀察下列點陣圖，并在⑤看面的黃線上寫出相應的等式．
①1=12
②1+3=22
③3+6=32
④6+10=42
⑤10+15=5210+15=52；
（4）通過猜想，寫出（3）中與第n個點陣相對應的等式（1+n-1）（n-1）2+（1+n）×n2=n2（1+n-1）（n-1）2+（1+n）×n2=n2；
（5）判斷225是不是正方形數，如果不是，說明理由；如果是，225可以看作哪兩個相鄰的“三角形數”之和？
（
1
+
2
）
×
2
2
（
1
+
3
）
×
3
2
（
1
+
4
）
×
4
2
（
1
+
4
）
×
4
2
（
1
+
9
）
×
9
2
（
1
+
9
）
×
9
2
（
1
+
n
-
1
）
（
n
-
1
）
2
（
1
+
n
）
×
n
2
（
1
+
n
-
1
）
（
n
-
1
）
2
（
1
+
n
）
×
n
2
【考點】規律型：數字的變化類；規律型：圖形的變化類．
【答案】1+2+3+4=；1+2+3+…+9=；10+15=52；+=n2
（
1
+
4
）
×
4
2
（
1
+
9
）
×
9
2
（
1
+
n
-
1
）
（
n
-
1
）
2
（
1
+
n
）
×
n
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：190引用：1難度：0.3
相似題
-
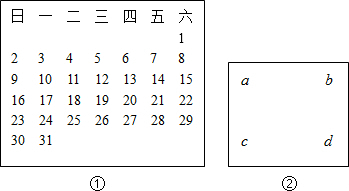
1．如圖是①2011年10月日歷，現用一長方形在日歷中任意框出4個數如圖②，請用一個等式表示a、b、c、d之間的關系：．
發布：2025/1/29 8:0:1組卷：56引用：2難度：0.7 -
2．“數學是將科學現象升華到科學本質認識的重要工具”，比如在化學中，甲烷的化學式CH4，乙烷的化學式是C2H6，丙烷的化學式是C3H8，…，設碳原子的數目為n（n為正整數），則它們的化學式都可用下列哪個式子來表示（ ）
發布：2024/12/6 13:0:3組卷：247引用：5難度：0.5 -
3．法國的“小九九”從“一一得一”到“五五二十五”和我國的“小九九”是一樣的，后面的就改用手勢了．右面兩個圖框是用法國“小九九”計算7×8和8×9的兩個示例．若用法國“小九九”計算7×9，左、右手依次伸出手指的個數是（ ）發布：2024/12/5 8:0:1組卷：182引用：3難度：0.9