問題背景
如圖1，AB，CD交于O，延長BD，CA交于E，∠B=∠C，證明：AEDE=BEEC；
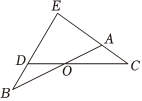
應(yīng)用拓展
如圖2，在四邊形ABCD中，AD∥BC，點E，F(xiàn)分別在邊CD，AB上，連BE，CF交于O，AE，DF交于T，
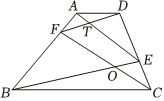
（1）若∠ABE=∠DCF，證明：∠AEB=∠DFC；
（2）若BE⊥CD于E，CF⊥AB于F，BCAD=n，sin∠ECO=m,直接寫出TETD= mnmn．
AE
DE
=
BE
EC
BC
AD
=
n
TE
TD
【考點】相似三角形的判定與性質(zhì)；解直角三角形．
【答案】mn
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/7/3 8:0:9組卷：208引用：1難度：0.5
相似題
-
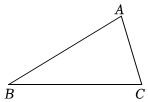1．如圖，在△ABC中，∠C＞∠B．
（1）請用尺規(guī)作圖法，在△ABC內(nèi)求作∠ACD，使∠ACD=∠B，CD交AB于D．（不要求寫作法，保留作圖痕跡）
（2）在（1）的條件下，若AC=6，AB=9，求AD的長．發(fā)布：2025/5/24 0:30:1組卷：35引用：1難度：0.6 -
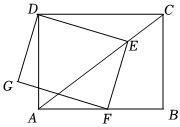2．如圖，在矩形ABCD中，AB=8，AD=6，點E是對角線AC上一動點，連接DE，過E作EF⊥DE，交AB邊于點F，以DE、EF為鄰邊作矩形DEFG．
（1）當(dāng)CE=4時，則EF的長為．
（2）點H在DC上，且HD=1，連接HG，則HG長的最小值是 ．發(fā)布：2025/5/24 0:30:1組卷：1054引用：3難度：0.5 -
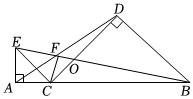3．如圖，點C在線段AB上，在AB同側(cè)作等腰Rt△ACE和等腰Rt△BCD，使∠EAC=∠BDC=90°，連接BE，分別交CD于點O，交AD于點F．
（1）求證：△ACD∽△ECB；
（2）若，AC=2，求AF的長．CB=42發(fā)布：2025/5/24 0:30:1組卷：233引用：1難度：0.5
相關(guān)試卷