2023年湖北省武漢一初慧泉中學中考數學模擬試卷（5月份）

一、選擇題（共10小題，每小題3分，共30分）

• 1．-2023的相反數是（　　）

  A． - 1 2023

  B．-2023

  C． 1 2023

  D．2023
  組卷：3613引用：387難度：0.9

  解析

• 2．如圖各交通標志中，不是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：139引用：10難度：0.9

  解析

• 3．“翻開人教版數學九年級下冊，恰好翻到第32頁”，這個事件是（　　）

  A．確定事件

  B．不可能事件

  C．必然事件

  D．隨機事件
  組卷：160引用：6難度：0.8

  解析

• 4．如圖是一個由5個相同的正方體組成的立體圖形，它的左視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：62引用：2難度：0.8

  解析

• 5．（2ab）³的結果是（　　）

  A．2ab6

  B．6a3b9

  C．8a3b3

  D．8ab9
  組卷：69引用：1難度：0.7

  解析

• 6．已知A（-1，y₁），B（-2，y₂），C（3，y₃）都在反比例函數

  y

  =

  k

  2

  +

  1

  x

  的圖象上，y₁、y₂、y₃的大小關系是（　　）

  A．y2＞y1＞y3

  B．y1＞y2＞y3

  C．y3＞y2＞y1

  D．y1＞y3＞y2
  組卷：154引用：2難度：0.8

  解析

• 7．已知m,n是一元二次方程x²-2x-5=0的兩根，則

  m

  -

  n

  m

  ?

  2

  m

  m

  -

  n

  的值是（　　）

  A．-2

  B．2

  C．-4

  D．4
  組卷：126引用：3難度：0.8

  解析

• 8．一個裝有進水管和出水管的容器，開始時，先打開進水管注水，3分鐘時，再打開出水管排水，8分鐘時，關閉進水管，直至容器中的水全部排完．在整個過程中，容器中的水量y（升）與時間x（分鐘）之間的函數關系如圖所示，則圖中a的值為（　　）

  A．10

  B． 29 3

  C． 28 3

  D．9
  組卷：1199引用：7難度：0.7

  解析

三、解答題（共8小題，共72分）

• 23．問題背景
  如圖1，AB，CD交于O，延長BD，CA交于E，∠B=∠C，證明：

  AE

  DE

  =

  BE

  EC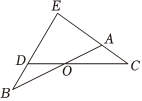

  ；
  
  應用拓展
  如圖2，在四邊形ABCD中，AD∥BC，點E，F分別在邊CD，AB上，連BE，CF交于O，AE，DF交于T，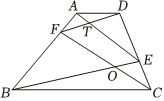
  
  （1）若∠ABE=∠DCF，證明：∠AEB=∠DFC；
  （2）若BE⊥CD于E，CF⊥AB于F，

  BC

  AD

  =

  n

  ，sin∠ECO=m,直接寫出

  TE

  TD

  =

  ．
  組卷：208引用：1難度：0.5

  解析

• 24．拋物線y=0.25x²+bx+c交x軸交于A，B兩點（A在B左側），與y軸交于C（0，-3），OB=3OA．
  
  （1）求拋物線的解析式；
  （2）若D是拋物線上B，C之間的一點（不與B，C重合），連接AD，BD，AD交y軸于E，記四邊形OEDB的面積為S，求S的最大值；
  （3）若M是第一象限拋物線上的一點，點N與M關于拋物線的對稱軸對稱，點T在第四象限拋物線上，且∠MTN=90°，若點M與點T的橫坐標之差為2，求點N的橫坐標．
  組卷：283引用：3難度：0.2

  解析