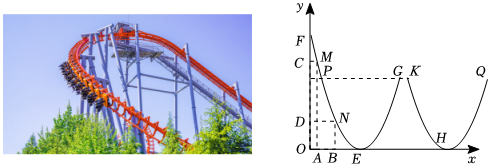
如圖所示，F→E→G為過山車的一部分軌道，它可以看成一段拋物線．其中OE=3米，OF=9米（軌道厚度忽略不計）
（1）求拋物線F→E→G的函數關系式；
（2）在軌道距離地面254米處有兩個位置P和G，當過山車運動到G處時，平行于地面向前運動了1米至K點，又進入下坡段K→H（K接口處軌道忽略不計）．已知軌道拋物線K→H→Q的形狀與拋物線P→E→G完全相同，在G到Q的運動過程中，當過山車距地面4米時，它離出發點的水平距離最遠有多遠？
（3）現需要在軌道下坡段F→E進行一種安全加固，建造某種材料的水平和豎直支架AM、CM、BN、DN，且要求AB=2OA．已知這種材料的價格是8000元/米，如何設計支架，會使造價最低？最低造價為多少元？
25
4
【考點】二次函數的應用．
【答案】（1）y=（x-3）2；
（2）11米；
（3）當OA=1米，OB=3米時造價最低，最低造價為64000元．
（2）11米；
（3）當OA=1米，OB=3米時造價最低，最低造價為64000元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/6 8:0:9組卷：213引用：3難度：0.5
相似題
-
1．對于豎直向上拋出的物體，在不考慮空氣阻力的情況下，有如下的關系式：
，其中h是物體上升的高度，v是拋出時的速度，g是重力加速度（g≈10m/s2），t是拋出后的時間．如果一物體以25m/s的初速度從地面豎直向上拋出，經過 秒鐘后它在離地面20m高的地方．h=vt-12gt2發布：2025/6/4 22:0:2組卷：133引用：2難度：0.6 -
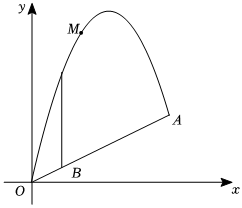2．如圖，一小球M（看作一個點）從斜坡OA上的O點處拋出，球的拋出路線是拋物線的一部分，建立如圖所示的平面直角坐標系，斜坡可以用一次函數y=x刻畫、若小球到達的最高的點坐標為（4，8），解答下列問題：12
（1）求拋物線的表達式；
（2）小球落點為A，求A點的坐標；
（3）在斜坡OA上的B點有一棵樹（樹高看成線段且垂直于x軸），B點的橫坐標為2，樹高為4，小球M能否飛過這棵樹？通過計算說明理由．發布：2025/6/5 0:30:1組卷：1188引用：8難度：0.4 -
3．某旅游公司在景區內配置了50輛觀光車供游客租賃使用，假定每輛觀光車一天內最多能出租一次，且每輛車的日租金x（元）是5的倍數，發現每天的營運規律如下：當x不超過100元時，觀光車能全部租出；當x超過100元時，每輛車的日租金每增加5元，租出去的觀光車就會減少1輛，已知所有觀光車每天的管理費是1100元．（注：凈收入=租車收入-管理費）
（1）當日租金x為135元時，觀光車能租出 輛；
（2）設每日凈收入為y元，寫出y與x的函數關系式；
（3）當每輛車的日租金為多少元時，每天的凈收入最多？發布：2025/6/5 5:30:2組卷：141引用：2難度：0.4