已知正方形ABCD，E，F為平面內兩點．

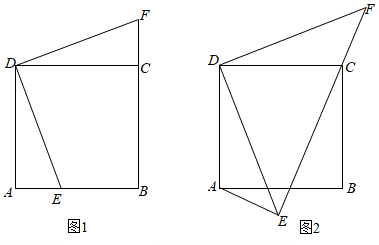
（探究建模）
（1）如圖1，當點E在邊AB上時，DE⊥DF，且B，C，F三點共線，求證：AE=CF；
（類比應用）
（2）如圖2，當點E在正方形ABCD外部時，DE⊥DF，AE⊥EF，且E，C，F三點共線．猜想并證明線段AE，CE，DE之間的數量關系；

【答案】（1）見解析；（2）猜想：EA+EC=

DE．理由見解析．

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：409引用：4難度：0.5

相似題

1．正方形ABCD中，AB=2，E為AB的中點，將△ADE沿DE折疊得到△FDE，FH⊥BC，垂足為H，則FH=
．
發布：2025/5/25 5:30:2組卷：606引用：4難度：0.5
解析
2．如圖，正方形ABCD的邊長為4，分別以正方形的三邊為直徑在正方形的內部作半圓，則陰影部分的面積等于
．
發布：2025/5/25 7:0:2組卷：244引用：3難度：0.5
解析
3．菱形ABCD的邊長為5，對角線AC、BD交于點O，AC=8，以AD為一邊作正方形ADEF，過點E作EG⊥直線BD，垂足為G，連接AG，則AG=
．
發布：2025/5/25 9:0:1組卷：130引用：5難度：0.6
解析

相關試卷

1．正方形ABCD中，AB=2，E為AB的中點，將△ADE沿DE折疊得到△FDE，FH⊥BC，垂足為H，則FH=．