部分高校開展基礎學科招生改革試點工作（強基計劃）的校考由試點高校自主命題，校考過程中達到筆試優秀才能進入面試環節．已知A、B兩所大學的筆試環節都設有三門考試科目且每門科目是否達到優秀相互獨立．若某考生報考A大學，每門科目達到優秀的概率均為25，若該考生報考B大學，每門科目達到優秀的概率依次為 14，25，n,其中0＜n＜1．
（1）若n=13，分別求出該考生報考A、B兩所大學在筆試環節恰好有一門科目達到優秀的概率；
（2）強基計劃規定每名考生只能報考一所試點高校，若以筆試過程中達到優秀科目個數的期望為依據作出決策，該考生更有希望進入A大學的面試環節，求n的范圍．
2
5
1
4
2
5
n
=
1
3
【考點】離散型隨機變量的均值（數學期望）．
【答案】（1）；；（2）0＜n＜．
54
125
9
20
11
20
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/23 12:26:7組卷：105引用：4難度：0.5
相似題
-
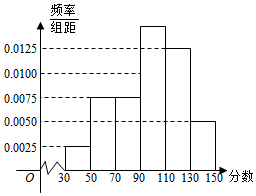1．某市舉行“中學生詩詞大賽”，分初賽和復賽兩個階段進行，規定：初賽成績大于90分的具有復賽資格，某校有800名學生參加了初賽，所有學生的成績均在區間（30，150]內，其頻率分布直方圖如圖．
（Ⅰ）求獲得復賽資格的人數；
（Ⅱ）從初賽得分在區間（110，150]的參賽者中，利用分層抽樣的方法隨機抽取7人參加學校座談交流，那么從得分在區間（110，130]與（130，150]各抽取多少人？
（Ⅲ）從（Ⅱ）抽取的7人中，選出3人參加全市座談交流，設X表示得分在區間（130，150]中參加全市座談交流的人數，求X的分布列及數學期望E（X）．發布：2024/12/29 13:30:1組卷：134引用：7難度：0.5 -
2．設離散型隨機變量X的分布列如表：
若離散型隨機變量Y=-3X+1，且E（X）=3，則（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 發布：2024/12/29 13:0:1組卷：199引用：6難度：0.5 -
3．從4名男生和2名女生中任選3人參加演講比賽，用X表示所選3人中女生的人數，則E（X）為（ ）
發布：2024/12/29 13:30:1組卷：139引用：6難度：0.7