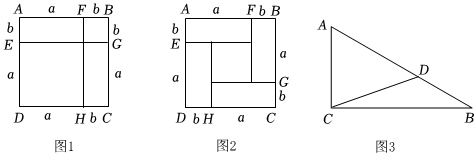
數學家波利亞說過：“為了得到一個方程，我們必須把同一個量以兩種不同的方法表示出來，即將一個量算兩次，從而建立相等關系，”這就是“算兩次”原理，換句話說，“算兩次”的思想是，對一個具體的量用方法甲來計算，得到的答案是A，而用方法乙計算則得到的答案是B，那么等式A=B成立．例如，我們運用“算兩次”的方法計算圖1中最大的正方形的面積，可以得到等式（a+b）²=a²+2ab+b²．
理解：
（1）如圖2，四個完全一樣的長方形擺成一個大的正方形，長方形的長和寬分別為a和b,運用“算兩次”的方法計算圖2中最大的正方形的面積，可以得到的等式是

（a+b）²=（a-b）²+4ab

（a+b）²=（a-b）²+4ab

（用a、b表示）
應用：
（2）利用（1）中的結論解決問題：若x+y=8，xy=4，則（x-y）²=

48

48

；
拓展：
（3）如圖3，已知Rt△ABC中，∠ACB=90°，AC=3，BC=4，AB=5，點D是AB上一動點．求CD的最小值．