如圖1，在正方形ABCD中，點G是對角線BD上一點，CG的延長線交AB于點E，交DA的延長線于點F，連接AG．
（1）求證：△AEG∽△FAG；
（2）若GE?GF=16，求GC的長．
（3）結(jié)合前兩步的解答，你能得出GE、GF和GC的數(shù)量關(guān)系嗎？如果把圖1中的正方形變?yōu)榱庑危溆鄺l件不變（如圖2），以上關(guān)系還成立嗎？（請直接寫出答案，不需要證明）
【考點】相似形綜合題．
【答案】（1）證明見解析過程；
（2）4；
（3）GC2=GE?GF，在圖2中仍成立．
（2）4；
（3）GC2=GE?GF，在圖2中仍成立．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/8/26 15:0:9組卷：87引用：2難度：0.2
相似題
-
1．數(shù)學(xué)課上，王老師出示問題：如圖1，將邊長為5的正方形紙片ABCD折疊，使頂點A落在邊CD上的點P處（點P與C、D不重合），折痕為EF，折疊后AB邊落在PQ的位置，PQ與BC交于點G．
（1）觀察操作結(jié)果，在圖1中找到一個與△DEP相似的三角形，并證明你的結(jié)論；
（2）當(dāng)點P在邊CD的什么位置時，△DEP與△CPG面積的比是9：25？請寫出求解過程；
（3）將正方形換成正三角形，如圖2，將邊長為5的正三角形紙片ABC折疊，使頂點A落在邊BC上的點P處（點P與B、C不重合），折痕為EF，當(dāng)點P在邊BC的什么位置時，△BEP與△CPF面積的比是9：25？請寫出求解過程．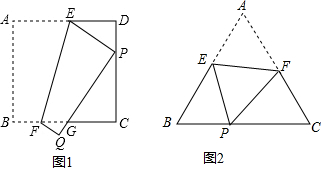
發(fā)布：2025/6/15 22:0:1組卷：1072引用：9難度：0.2 -
2．在△ABC中，CD是中線，E，F(xiàn)分別為BC，AC上的一點，連接EF交CD于點P．
（1）如圖1，若F為AC的中點，CE=2BE，求的值；DFEC
（2）如圖2，設(shè)=m,CEBC=n（n＜CFAC），若m+n=4mn,求證：PD=PC；12
（3）如圖3，F(xiàn)為AC的中點，連接AE交CD于點Q，若QD=QP，直接寫出的值．BEEC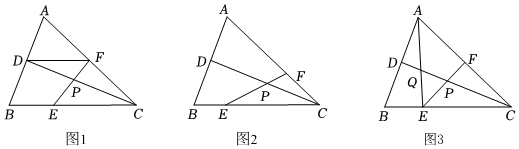
發(fā)布：2025/6/15 15:0:1組卷：334引用：2難度：0.3 -
3．矩形ABCD中，AB=nAD（n＞1），點P為對角線AC上的一個動點（不與A、C兩點重合），過點P作直線MN⊥AC，分別交射線AB、射線AD于點M、N．
（1）如圖1，當(dāng)點N與點D重合時，求的值（用含有n的代數(shù)式表示）．PMPD
（2）如圖2，當(dāng)點M為AB邊的中點，且DP=DA時，求n的值．
（3）如圖3，當(dāng)n=2，移動點P，使得△APD與△BPC相似，則的值=．AMAD
發(fā)布：2025/6/15 15:0:1組卷：107引用：1難度：0.2